
已知函數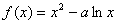 在
在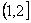 是增函數,
是增函數,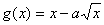 在
在 為減函數.
為減函數.
(1)求 ,
, 的表達式;
的表達式;
(2)求證:當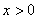 時,方程
時,方程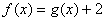 有唯一解;
有唯一解;
(3)當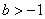 時,若
時,若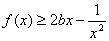 在
在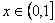 內恒成立,求
內恒成立,求 的取值范圍.
的取值范圍.
解(1)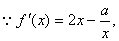 依題意
依題意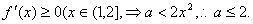 2分
2分
又∵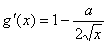 ,依題意
,依題意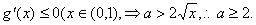 ……………3分
……………3分
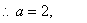
 ……………………………………4分
……………………………………4分
(2)由(1)可知,原方程為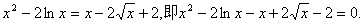
設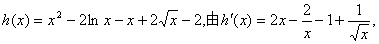 …………………5分
…………………5分
令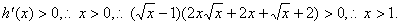
令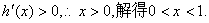 ………………………………………7分
………………………………………7分
由
|
|
(0,1) |
1 |
(1,+∞) |
|
|
- |
0 |
+ |
|
|
遞減 |
0 |
遞增 |
即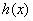 在
在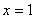 處有一個最小值0,即當
處有一個最小值0,即當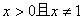 時,
時,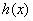 >0,
>0, 只有一個解.
只有一個解.
即當x>0時,方程 有唯一解. ………………………………………8分
有唯一解. ………………………………………8分
(3)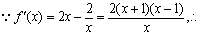 當
當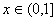 時,
時,
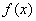 為減函數,其最小值為1.
………………………………………9分
為減函數,其最小值為1.
………………………………………9分
令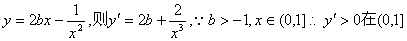 恒成立…………10分
恒成立…………10分
∴函數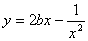 在
在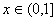 為增函數,其最大值為2b-1,…………………11分
為增函數,其最大值為2b-1,…………………11分
依題意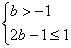 ,解得
,解得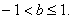 為所求范圍. …………………………………12分
為所求范圍. …………………………………12分


科目:高中數學 來源: 題型:
| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源:2008-2009學年廣東省深圳市福田實驗學校高二(下)第四次段考數學試卷(文科)(解析版) 題型:解答題
查看答案和解析>>
科目:高中數學 來源:2011-2012學年遼寧省沈陽市四校協作體高三(上)12月月考數學試卷(理科)(解析版) 題型:解答題
 .
. 是增函數,當|m|最小時,求m的值.
是增函數,當|m|最小時,求m的值.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com