
 已知函數f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其導函數的圖象f'(x)如圖所示,則$f({\frac{π}{2}})$的值為( )
已知函數f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其導函數的圖象f'(x)如圖所示,則$f({\frac{π}{2}})$的值為( )| A. | $2\sqrt{3}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 4 |
分析 求出函數的導函數,利用導函數的周期,求出ω,利用振幅求出A,利用導函數經過($\frac{3π}{2}$,-2),求出φ,得到函數的解析式,即可得解.
解答 解:函數的導函數f′(x)=ωAcos(ωx+φ),由圖象可知f′(x)的周期為4π.
所以ω=$\frac{1}{2}$.
又因為Aω=2.
所以A=4.
函數經過($\frac{3π}{2}$,-2),
所以-2=2cos($\frac{1}{2}$×$\frac{3π}{2}$+φ),0<φ<π,
所以 $\frac{1}{2}$×$\frac{3π}{2}$+φ=π,即φ=$\frac{π}{4}$.
所以f(x)=4sin($\frac{1}{2}$x+$\frac{π}{4}$).
所以f($\frac{π}{2}$)=4sin($\frac{1}{2}$×$\frac{π}{2}$+$\frac{π}{4}$)=4.
故選:D.
點評 本題主要考查函數的導數與函數的圖象的關系,考查計算能力和數形結合思想的應用,屬于中檔題.


 新課標快樂提優暑假作業陜西旅游出版社系列答案
新課標快樂提優暑假作業陜西旅游出版社系列答案 暑假銜接培優教材浙江工商大學出版社系列答案
暑假銜接培優教材浙江工商大學出版社系列答案科目:高中數學 來源: 題型:選擇題
| x | 1 | 2 | 1.5 | 1.75 | 1.625 | 1.6875 |
| f(x) | -5.00 | 4.00 | -1.63 | 0.86 | -0.46 | 0.18 |
| A. | 1.50 | B. | 1.66 | C. | 1.70 | D. | 1.75 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
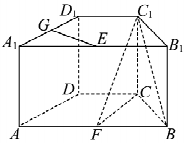 如圖,在直四棱柱ABCD-A1B1C1D1中,底面ABCD為等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、F、G分別是棱A1B1、AB、A1D1的中點.
如圖,在直四棱柱ABCD-A1B1C1D1中,底面ABCD為等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、F、G分別是棱A1B1、AB、A1D1的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
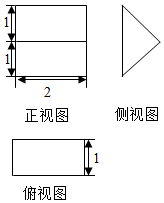 《九章算術》中,將底面是直角三角形的直三棱柱稱之為“塹堵”,已知某“塹堵”的三視圖如圖所示,則該“塹堵”的表面積為( )
《九章算術》中,將底面是直角三角形的直三棱柱稱之為“塹堵”,已知某“塹堵”的三視圖如圖所示,則該“塹堵”的表面積為( )| A. | 2 | B. | 4 | C. | 4+4$\sqrt{2}$ | D. | 6+4$\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com