
設(shè)橢圓![]() 過點(diǎn)
過點(diǎn)![]() ,且左焦點(diǎn)為
,且左焦點(diǎn)為![]()
(Ⅰ)求橢圓C的方程;
(Ⅱ)當(dāng)過點(diǎn)P(4,1)的動(dòng)直線l與橢圓C相交于兩不同點(diǎn)A,B時(shí),在線段AB上取點(diǎn)Q,滿足![]() .證明:點(diǎn)Q總在某定直線上.
.證明:點(diǎn)Q總在某定直線上.
解析:(Ⅰ)由題意: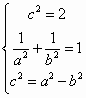 ,解得
,解得![]() .
.
所求的求橢圓![]() 的方程
的方程![]() .
.
(Ⅱ)方法一:設(shè)點(diǎn)![]() ,
,![]() ,
,![]() ,由題設(shè),
,由題設(shè),![]() 、
、![]() 、
、![]() 、
、![]() 均不為0,且
均不為0,且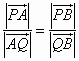 ,又
,又![]() 四點(diǎn)共線,可設(shè)
四點(diǎn)共線,可設(shè)![]() ,
,![]() ,于是
,于是
![]() ,
,![]() ①
①
![]() ,
,![]() ②
②
由于![]() ,
,![]() 在橢圓上,將①②分別帶入
在橢圓上,將①②分別帶入![]() 的方程
的方程![]() ,整理得:
,整理得:
![]() ③
③
![]() ④
④
由④-③得![]() .
.
∵![]() ,∴
,∴![]() .即點(diǎn)
.即點(diǎn)![]() 總在直線
總在直線![]() 上.
上.
方法二:設(shè)點(diǎn)![]() ,
,![]() ,
,![]() ,由題設(shè),
,由題設(shè),![]() 、
、![]() 、
、![]() 、
、![]() 均不為0,記
均不為0,記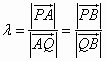 ,則
,則![]() 且
且![]() .
.
又![]() 四點(diǎn)共線,從而
四點(diǎn)共線,從而![]() ,
,![]() ,于是:
,于是:
![]() ,
,![]() ;
;
![]() ,
,![]() .
.
從而![]() ①
①
![]() ②
②
又點(diǎn)![]() 在橢圓上,即
在橢圓上,即
![]() ③
③
![]() ④
④
①+2![]() ②并結(jié)合③,④得
②并結(jié)合③,④得![]() ,即點(diǎn)
,即點(diǎn)![]() 總在直線
總在直線![]() 上.
上.
本題主要考查直線、橢圓的方程及幾何性質(zhì)、線段的定比分點(diǎn)等基礎(chǔ)知識(shí)、基本方法和分析問題、解決問題的能力.本小題滿分13分.


 學(xué)而優(yōu)暑期銜接南京大學(xué)出版社系列答案
學(xué)而優(yōu)暑期銜接南京大學(xué)出版社系列答案 Happy holiday歡樂假期暑假作業(yè)廣東人民出版社系列答案
Happy holiday歡樂假期暑假作業(yè)廣東人民出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
(08年安徽卷理) (本小題滿分13分)
設(shè)橢圓![]() 過點(diǎn)
過點(diǎn)![]() ,且左焦點(diǎn)為
,且左焦點(diǎn)為![]()
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)當(dāng)過點(diǎn)![]() 的動(dòng)直線
的動(dòng)直線![]() 與橢圓
與橢圓![]() 相交于兩不同點(diǎn)
相交于兩不同點(diǎn)![]() 時(shí),在線段
時(shí),在線段![]() 上取點(diǎn)
上取點(diǎn)![]() ,滿足
,滿足![]() 。證明:點(diǎn)Q總在某定直線上。
。證明:點(diǎn)Q總在某定直線上。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
設(shè)橢圓![]() 過點(diǎn)
過點(diǎn)![]() ,且左焦點(diǎn)為
,且左焦點(diǎn)為![]()
(Ⅰ)求橢圓C的方程;
(Ⅱ)當(dāng)過點(diǎn)P(4,1)的動(dòng)直線l與橢圓C相交于兩不同點(diǎn)A,B時(shí),在線段AB上取點(diǎn)Q,滿足![]() 。證明:點(diǎn)Q總在某定直線上。
。證明:點(diǎn)Q總在某定直線上。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010年廣東省高考數(shù)學(xué)考點(diǎn)預(yù)測(cè):解析幾何(解析版) 題型:解答題
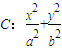 =1(a>b>0)過點(diǎn)
=1(a>b>0)過點(diǎn)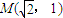 ,且左焦點(diǎn)為
,且左焦點(diǎn)為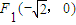
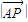 •
•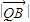 =
=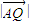 •
•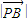 ,證明:點(diǎn)Q總在某定直線上.
,證明:點(diǎn)Q總在某定直線上.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2008年安徽省高考數(shù)學(xué)試卷(理科)(解析版) 題型:解答題
 =1(a>b>0)過點(diǎn)
=1(a>b>0)過點(diǎn)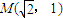 ,且左焦點(diǎn)為
,且左焦點(diǎn)為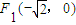
 •
•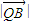 =
=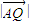 •
•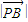 ,證明:點(diǎn)Q總在某定直線上.
,證明:點(diǎn)Q總在某定直線上.查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com