
�E�A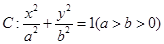 ���x���ʞ�
���x���ʞ� ���ɽ��c(di��n)�քe��
���ɽ��c(di��n)�քe��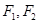 ���c(di��n)
���c(di��n)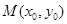 �ǙE�AC��һ�c(di��n)��
�ǙE�AC��һ�c(di��n)��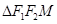 �����L(zh��ng)��16���O(sh��)����MO��O������(bi��o)ԭ�c(di��n)���c�A
�����L(zh��ng)��16���O(sh��)����MO��O������(bi��o)ԭ�c(di��n)���c�A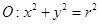 �����c(di��n)N���Ҿ���MN�L(zh��ng)�ȵ���Сֵ��
�����c(di��n)N���Ҿ���MN�L(zh��ng)�ȵ���Сֵ��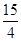 .
.
��1����E�AC�Լ��AO�ķ��̣�
��2����(d��ng)�c(di��n)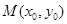 �ڙE�AC���\(y��n)��(d��ng)�r(sh��)���Д�ֱ��
�ڙE�AC���\(y��n)��(d��ng)�r(sh��)���Д�ֱ��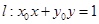 �c�AO��λ���P(gu��n)ϵ.
�c�AO��λ���P(gu��n)ϵ.
��1��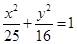
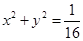
��2��ֱ��l�c�AO�ཻ
��������
ԇ�}�������⣺��1���O(sh��)�E�AC�İ뽹����c���t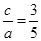 ����
����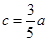 ��
1��
��
1��
��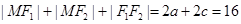 ��
2��
��
2��
(li��n)���٢ڣ����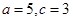 ������
������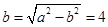 .
.
���ԙE�AC�ķ��̞�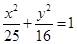 .
4��
.
4��
���E�AC���c(di��n)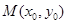 �c�E�A����O�ľ��x��
�c�E�A����O�ľ��x��
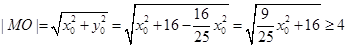 ����̖(h��o)��
����̖(h��o)��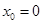 �r(sh��)��������6��
�r(sh��)��������6��
��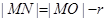 ���t
���t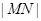 ����Сֵ��
����Сֵ��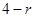 ���Ķ�
���Ķ�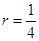 ���t�AO�ķ��̞�
���t�AO�ķ��̞�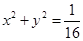 . 8��
. 8��
��2����?y��n)��c(di��n)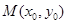 �ڙE�AC���\(y��n)��(d��ng)������
�ڙE�AC���\(y��n)��(d��ng)������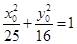 .��
.��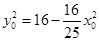 .
.
�A��O��ֱ��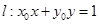 �ľ��x
�ľ��x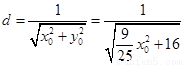 .
11��
.
11��
��(d��ng)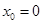 ��
��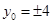 ��
��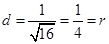 ���tֱ��l�c�AO����.
���tֱ��l�c�AO����.
��(d��ng)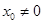 ��
��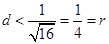 ���tֱ��l�c�AO�ཻ.
14��
���tֱ��l�c�AO�ཻ.
14��
���c(di��n)��ֱ���c�A���P(gu��n)ϵ���E�A�ķ���
�c(di��n)�u(p��ng)����Ҫ�ǿ����˙E�A�����|(zh��)���\(y��n)�ã��Լ��A�ķ��̣���ֱ���c�A��λ���P(gu��n)ϵ�����ڻ��A(ch��)�}��


 �p����ٿ���(f��)��(x��)ϵ�д�
�p����ٿ���(f��)��(x��)ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
��D����ֱ������(bi��o)ϵ![]() �У���֪�E�A
�У���֪�E�A![]() ���x����e��
���x����e��![]() �����҃ɂ�(g��)���քe��
�����҃ɂ�(g��)���քe��![]() ���^�ҽ��c(di��n)
���^�ҽ��c(di��n)![]() ���c
���c![]() �S��ֱ��
�S��ֱ��
ֱ���c�E�A![]() �ཻM��N���c(di��n)����|MN|=1��
�ཻM��N���c(di��n)����|MN|=1��
(��) ��E�A![]() �ķ��̣�
�ķ��̣�
(��) �O(sh��)�E�A![]() ������c(di��n)��A,����c(di��n)��B����(d��ng)�c(di��n)P�M��
������c(di��n)��A,����c(di��n)��B����(d��ng)�c(di��n)P�M��![]() ��
��
��![]() ��ԇ���c(di��n)P��܉�E���̣�ʹ�c(di��n)B�P(gu��n)��ԓ܉�E�Č�(du��)�Q�c(di��n)���ڙE�A
��ԇ���c(di��n)P��܉�E���̣�ʹ�c(di��n)B�P(gu��n)��ԓ܉�E�Č�(du��)�Q�c(di��n)���ڙE�A![]() ��.
��. ![]()

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
��D����ֱ������(bi��o)ϵ![]() �У���֪�E�A
�У���֪�E�A![]() ���x����e��
���x����e��![]() �����҃ɂ�(g��)���քe��
�����҃ɂ�(g��)���քe��![]() ���^�ҽ��c(di��n)
���^�ҽ��c(di��n)![]() ���c
���c![]() �S��ֱ��
�S��ֱ��
ֱ���c�E�A![]() �ཻM��N���c(di��n)����|MN|=1��
�ཻM��N���c(di��n)����|MN|=1��
(��) ��E�A![]() �ķ��̣�
�ķ��̣�
(��) �O(sh��)�E�A![]() ������c(di��n)��A,����c(di��n)��B����(d��ng)�c(di��n)P�M��
������c(di��n)��A,����c(di��n)��B����(d��ng)�c(di��n)P�M��![]() ��
��
��![]() ��ԇ���c(di��n)P��܉�E���̣�ʹ�c(di��n)B�P(gu��n)��ԓ܉�E�Č�(du��)�Q�c(di��n)���ڙE�A
��ԇ���c(di��n)P��܉�E���̣�ʹ�c(di��n)B�P(gu��n)��ԓ܉�E�Č�(du��)�Q�c(di��n)���ڙE�A![]() ��.
��. ![]()

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ��2013�ñ����Ж|�Dž^(q��)����12��(li��n)�����Ɣ�(sh��)�W(xu��)ԇ���������棩 �}�ͣ�����}
��֪�E�A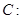
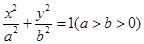 ���x���ʞ�
���x���ʞ�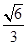 ���E�A���S��һ��(g��)���c(di��n)�c�ɂ�(g��)��
���E�A���S��һ��(g��)���c(di��n)�c�ɂ�(g��)��
������E�A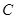 �ķ��̣�
�ķ��̣�
������֪?ji��ng)�ֱ��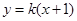 �c�E�A
�c�E�A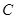 �ཻ��
�ཻ��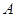 ��
��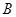 ���c(di��n). ��������
���c(di��n). ��������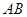 ���c(di��n)��
���c(di��n)��
�M����(bi��o)��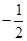 �����
����б��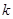 ��ֵ�������c(di��n)
��ֵ�������c(di��n)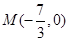 �����C��
�����C��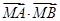 �鶨ֵ.
�鶨ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
��֪�E�A![]()
![]() ���x���ʞ�
���x���ʞ�![]() ���E�A���S��һ��(g��)���c(di��n)�c�ɂ�(g��)��
���E�A���S��һ��(g��)���c(di��n)�c�ɂ�(g��)��
�c(di��n)��(g��u)�ɵ������ε���e��![]() .
.
������E�A![]() �ķ��̣�
�ķ��̣�
������֪?ji��ng)�ֱ��![]() �c�E�A
�c�E�A![]() �ཻ��
�ཻ��![]() ��
��![]() ���c(di��n). ��������
���c(di��n). ��������![]() ���c(di��n)��
���c(di��n)��
�M����(bi��o)��![]() �����
����б��![]() ��ֵ�������c(di��n)
��ֵ�������c(di��n)![]() �����C��
�����C��![]() �鶨ֵ.
�鶨ֵ.
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com