
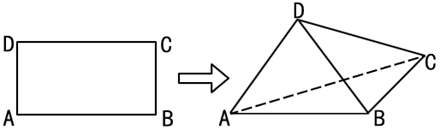
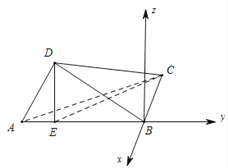
【題目】如圖,四邊形![]() 是矩形,沿對角線
是矩形,沿對角線![]() 將
將![]() 折起,使得點
折起,使得點![]() 在平面
在平面![]() 上的射影恰好落在邊
上的射影恰好落在邊![]() 上.
上.
(1)求證:平面![]() 平面
平面![]() ;
;
(2)當![]() 時,求二面角
時,求二面角![]() 的余弦值.
的余弦值.
【答案】(I)見解析;(II)![]() .
.
【解析】試題分析:(1)先證明![]() . 結合
. 結合![]() ,得
,得![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
(2)以點![]() 為原點,線段
為原點,線段![]() 所在的直線為
所在的直線為![]() 軸,線段
軸,線段![]() 所在的直線為
所在的直線為![]() 軸,建立空間直角坐標系,用向量法求解即可.
軸,建立空間直角坐標系,用向量法求解即可.
試題解析:(1)設點![]() 在平面
在平面![]() 上的射影為點
上的射影為點![]() ,連接
,連接![]()
則![]() 平面
平面![]() ,所以
,所以![]() .
.
因為四邊形![]() 是矩形,所以
是矩形,所以![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
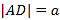
(2)方法1:在矩形![]() 中,過點
中,過點![]() 作
作![]() 的垂線,垂足為
的垂線,垂足為![]() ,連結
,連結![]() .
.
因為![]() 平面
平面![]()
![]() ,又DM∩DE=D
,又DM∩DE=D
所以![]() 平面
平面![]()
![]() ,
,
所以![]() 為二面角
為二面角![]() 的平面角.
的平面角.
設![]() ,則
,則![]() .
.
在![]() 中,易求出
中,易求出![]() ,
, ![]() .
.
在![]() 中,
中, ![]() ,
,
所以![]() .
.
方法2:以點![]() 為原點,線段
為原點,線段![]() 所在的直線為
所在的直線為![]() 軸,線段
軸,線段![]() 所在的直線為
所在的直線為![]() 軸,建立空間直角坐標系,如圖所示.
軸,建立空間直角坐標系,如圖所示.
設![]() ,則
,則![]() ,所以
,所以![]() ,
, ![]() .
.
由(I)知![]() ,又
,又![]() ,所以
,所以![]() °,
°,![]() °,那么
°,那么![]() ,
, ![]() ,
, ![]() ,
,
所以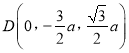 ,所以
,所以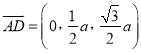 ,
, ![]() .
.
設平面![]() 的一個法向量為
的一個法向量為![]() ,則
,則![]() 即
即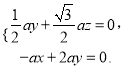
取![]() ,則
,則![]() ,
, ![]() ,所以
,所以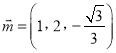 .
.
因為平面![]() 的一個法向量為
的一個法向量為![]() ,
,
所以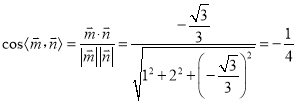 .
.
所以求二面角![]() 的余弦值為
的余弦值為![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】如圖,四邊形ABCD為平行四邊形,點E在AB上,AE=2EB=2,且DE⊥AB.以DE為折痕把△ADE折起,使點A到達點F的位置,且∠FEB=60°.
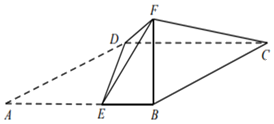
(1)求證:平面BFC⊥平面BCDE;
(2)若直線DF與平面BCDE所成角的正切值為![]() ,求二面角E﹣DF﹣C的正弦值.
,求二面角E﹣DF﹣C的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為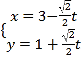 (
(![]() 為參數),在以坐標原點為極點,
為參數),在以坐標原點為極點,![]() 軸正半軸為極軸的極坐標系中,曲線
軸正半軸為極軸的極坐標系中,曲線![]() 的方程為
的方程為![]() .
.
(1)求曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設曲線![]() 與直線
與直線![]() 交于點
交于點![]() ,點
,點![]() 的坐標為(3,1),求
的坐標為(3,1),求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,隨著“霧霾”天出現的越來越頻繁,很多人為了自己的健康,外出時選擇戴口罩,長郡中學高三興趣研究小組利用暑假空閑期間做了一項對人們霧霾天外出時是否戴口罩的調查,共調查了120人,其中女性70人,男性50人,并根據統計數據畫出等高條形圖如圖所示:
(Ⅰ)利用圖形判斷性別與霧霾天外出戴口罩是否有關系;
(Ⅱ)根據統計數據建立一個![]() 列聯表;
列聯表;
(Ⅲ)能否在犯錯誤的概率不超過0.05的前提下認為性別與霧霾天外出戴口罩有關系.
附: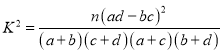

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】金秋九月,丹桂飄香,某高校迎來了一大批優秀的學生.新生接待其實也是和社會溝通的一個平臺.校團委、學生會從在校學生中隨機抽取了160名學生,對是否愿意投入到新生接待工作進行了問卷調查,統計數據如下:
愿意 | 不愿意 | |
男生 | 60 | 20 |
女士 | 40 | 40 |
(1)根據上表說明,能否有99%把握認為愿意參加新生接待工作與性別有關;
(2)現從參與問卷調查且愿意參加新生接待工作的學生中,采用按性別分層抽樣的方法,選取10人.若從這10人中隨機選取3人到火車站迎接新生,設選取的3人中女生人數為![]() ,寫出
,寫出![]() 的分布列,并求
的分布列,并求![]() .
.
附: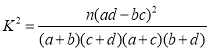 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】扇形AOB中心角為![]() ,所在圓半徑為
,所在圓半徑為![]() ,它按如圖(Ⅰ)(Ⅱ)兩種方式有內接矩形CDEF.
,它按如圖(Ⅰ)(Ⅱ)兩種方式有內接矩形CDEF.

(1)矩形CDEF的頂點C、D在扇形的半徑OB上,頂點E在圓弧AB上,頂點F在半徑OA上,設![]() ;
;
(2)點M是圓弧AB的中點,矩形CDEF的頂點D、E在圓弧AB上,且關于直線OM對稱,頂點C、F分別在半徑OB、OA上,設![]() ;
;
試研究(1)(2)兩種方式下矩形面積的最大值,并說明兩種方式下哪一種矩形面積最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在黨中央的正確指導下,通過全國人民的齊心協力,特別是全體一線醫護人員的奮力救治,二月份“新冠肺炎”疫情得到了控制.下圖是國家衛健委給出的全國疫情通報,甲、乙兩個省份從2月7日到2月13日一周的新增“新冠肺炎”確診人數的折線圖如下:

根據圖中甲、乙兩省的數字特征進行比對,通過比較把你得到最重要的兩個結論寫在答案紙指定的空白處.
①_________________________________________________.
②_________________________________________________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“中國剩余定理”又稱“孫子定理”.1852年,英國來華傳教士偉烈亞力將《孫子算經》中“物不知數”問題的解法傳至歐洲.1874年,英國數學家馬西森指出此法符合1801年由高斯得到的關于同余式解法的一般性定理,因而西方稱之為“中國剩余定理”.“中國剩余定理”講的是一個關于整除的問題,現有這樣一個整除問題:將1到2019這2019個數中,能被3除余2且被5整除余2的數按從小到大的順序排成一列,構成數列![]() ,則此數列所有項中,中間項的值為( )
,則此數列所有項中,中間項的值為( )
A.992B.1022C.1007D.1037
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com