
【題目】設等差數列{an}的前n項和為Sn,若Sm-1=-2,Sm=0,Sm+1=3,則m=( )
A. 5 B. 4 C. 3 D. 6
【答案】A
【解析】
根據數列前n項和的定義得到![]() 的值,再由數列的前n項和的公式得到
的值,再由數列的前n項和的公式得到![]() ,進而求得首項,由
,進而求得首項,由![]() =2,解得m值.
=2,解得m值.
Sm-1=-2,Sm=0,故得到![]() Sm=0,Sm+1=3,則
Sm=0,Sm+1=3,則![]() ,
,
根據等差數列的前n項和公式得到Sm=![]() ,得到首項為-2,故
,得到首項為-2,故![]() =2,解得m=5.
=2,解得m=5.
故答案為:A.
【點睛】
這個題目考查的是數列通項公式的求法及數列求和的常用方法;數列通項的求法中有常見的已知![]() 和
和![]() 的關系,求
的關系,求![]() 表達式,一般是寫出
表達式,一般是寫出![]() 做差得通項,但是這種方法需要檢驗n=1時通項公式是否適用;數列求和常用法有:錯位相減,裂項求和,分組求和等。
做差得通項,但是這種方法需要檢驗n=1時通項公式是否適用;數列求和常用法有:錯位相減,裂項求和,分組求和等。
【題型】單選題
【結束】
11
【題目】已知等比數列{an}的各項均為不等于1的正數,數列{bn}滿足bn=lgan,b3=18,b6=12,則數列{bn}的前n項和的最大值等于( )
A. 126 B. 130 C. 132 D. 134
【答案】C
【解析】
由題意可知,lga3=b3,lga6=b6再由b3,b6,用a1和q表示出a3和b6,進而求得q和a1,根據{an}為正項等比數列推知{bn}為等差數列,進而得出數列bn的通項公式和前n項和,可知Sn的表達式為一元二次函數,根據其單調性進而求得Sn的最大值.
由題意可知,lga3=b3,lga6=b6.
又∵b3=18,b6=12,則a1q2=1018,a1q5=1012,
∴q3=10﹣6.
即q=10﹣2,∴a1=1022.
又∵{an}為正項等比數列,
∴{bn}為等差數列,
且d=﹣2,b1=22.
故bn=22+(n﹣1)×(﹣2)=﹣2n+24.
∴Sn=22n+![]() ×(﹣2)
×(﹣2)
=﹣n2+23n=![]() ,又∵n∈N*,故n=11或12時,(Sn)max=132.
,又∵n∈N*,故n=11或12時,(Sn)max=132.
故答案為:C.


 名校聯盟快樂課堂系列答案
名校聯盟快樂課堂系列答案 黃岡創優卷系列答案
黃岡創優卷系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax2+ ![]() +5(常數a,b∈R)滿足f(1)+f(﹣1)=14.
+5(常數a,b∈R)滿足f(1)+f(﹣1)=14.
(1)求出a的值,并就常數b的不同取值討論函數f(x)奇偶性;
(2)若f(x)在區間(﹣∞,﹣ ![]() )上單調遞減,求b的最小值;
)上單調遞減,求b的最小值;
(3)在(2)的條件下,當b取最小值時,證明:f(x)恰有一個零點q且存在遞增的正整數數列{an},使得 ![]() =q
=q ![]() +q
+q ![]() +q
+q ![]() +…+q
+…+q ![]() +…成立.
+…成立.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知{an}為等比數列,a4+a7=2,a5a6=-8,則a1+a10=( )
A. 7 B. 5
C. -5 D. -7
【答案】D
【解析】由![]() 解得
解得![]() 或
或![]()
∴![]() 或
或 ,∴a1+a10=a1(1+q9)=-7.選D.
,∴a1+a10=a1(1+q9)=-7.選D.
點睛:在解決等差、等比數列的運算問題時,有兩個處理思路,一是利用基本量,將多元問題簡化為一元問題,雖有一定量的運算,但思路簡潔,目標明確;二是利用等差、等比數列的性質,性質是兩種數列基本規律的深刻體現,是解決等差、等比數列問題既快捷又方便的工具,應有意識地去應用.但在應用性質時要注意性質的前提條件,有時需要進行適當變形. 在解決等差、等比數列的運算問題時,經常采用“巧用性質、整體考慮、減少運算量”的方法.
【題型】單選題
【結束】
8
【題目】在數列{ ![]() }中,已知
}中,已知![]() ,
,![]() ,
,![]() ,則
,則![]() 等于( )
等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)是定義在R上的奇函數,當x>0時,f(x)=x﹣1,則不等式f(x)<0的解集為( ) 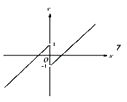
A.(﹣∞,﹣1)∪(0,1)
B.(﹣∞,﹣1)∪(1,+∞)
C.(﹣1,1)
D.(﹣1,0)∪(1,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓E: ![]() =1(a>b>0)的焦距為2
=1(a>b>0)的焦距為2 ![]() ,其上下頂點分別為C1 , C2 , 點A(1,0),B(3,2),AC1⊥AC2 .
,其上下頂點分別為C1 , C2 , 點A(1,0),B(3,2),AC1⊥AC2 .
(1)求橢圓E的方程及離心率;
(2)點P的坐標為(m,n)(m≠3),過點A任意作直線l與橢圓E相交于點M,N兩點,設直線MB,BP,NB的斜率依次成等差數列,探究m,n之間是否滿足某種數量關系,若是,請給出m,n的關系式,并證明;若不是,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com