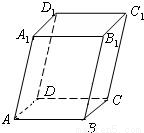
分析:由平行六面體的體積公式:V=Sh,其中S為底面面積,h為底面上的高,使用向量法時,若以平面AC為底面,不難得到V=
||•||•||•cosα•sinβ(其中α為
與底面法向量的夾角,β為
與
的夾角.由向量的“×”運算的定義及向量數量積運算的定義,不難得到:V=|
•(
×
)|考慮到平面AD
1、平面AB
1也可以看成底面故由此可類比推理得到三個類似的公式.
解答:解:若以平面AC為底面,不難得到:
V=
||•||•||•cosα•sinβ(其中α為
與底面法向量的夾角,β為
與
的夾角)
由向量的“×”運算的定義及向量數量積運算的定義,不難得到:
V=|
•(
×
)|
考慮到平面AD
1、平面AB
1也可以看成底面故由此可類比推理得:
V=|
•(
×
)|=
|•(×)|=
|•(×)|故答案為:
|•(×)|或
|•(×)|,或
|•(×)| 點評:類比推理的一般步驟是:(1)找出兩類事物之間的相似性或一致性;(2)用一類事物的性質去推測另一類事物的性質,得出一個明確的命題(猜想).另外,在本題的解答過程中,V=
||•||•||•cosα•sinβ(其中α為
與底面法向量的夾角,β為
與
的夾角)也是很關鍵的,可能文科學生沒有空間向量的概念,故建議文科學生可以簡單了解一個關于空間向量運算的知識.

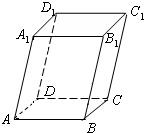 定義向量運算“×”:
定義向量運算“×”:

 名師點撥卷系列答案
名師點撥卷系列答案 英才計劃期末調研系列答案
英才計劃期末調研系列答案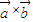 的結果為一個向量,其模為
的結果為一個向量,其模為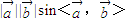 ,且
,且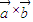 與向量
與向量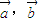 均垂直.則右圖平行六面體ABCD-A1B1C1D1的體積用
均垂直.則右圖平行六面體ABCD-A1B1C1D1的體積用 表示為 .
表示為 .