
(本題滿分11分)在△ABC中,內角A,B,C對邊的邊長分別是a,b,c,已知c=2,C=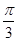 .
.
(1)若△ABC的面積等于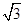 ,求a,b;
,求a,b;
(2)若sinC+sin(B-A)=2sin2A,求△ABC的面積.
(1)a=2,b=2.(2)S= absinC=
absinC= .
.
【解析】
試題分析:(1)由余弦定理及已知條件得,a2+b2-ab=4,…………2分
又因為△ABC的面積等于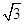 ,所以
,所以 absinC=
absinC=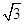 ,得ab=4.…………4分
,得ab=4.…………4分
聯立方程組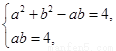 解得a=2,b=2.…………5分
解得a=2,b=2.…………5分
(2)由題意得sin(B+A)+sin(B-A)=4sinAcosA,即sinBcosA=2sinAcosA,…………7分
當cosA=0時,A=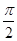 ,B=
,B= ,a=
,a=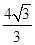 ,b=
,b= ,…………8分
,…………8分
當cosA≠0時,得sinB=2sinA,由正弦定理得b=2a,聯立方程組
解得a= ,b=
,b=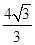 .…………10分
.…………10分
所以△ABC的面積S= absinC=
absinC= .…………11分
.…………11分
考點:本題主要考查正弦定理、余弦定理的應用,三角形內角和定理,兩角和差的三角函數。
點評:典型題,本題在考查正弦定理、余弦定理的應用,三角形內角和定理,兩角和差的三角函數的同時,考查了函數方程思想,在兩道小題中,均通過建立方程組,以便求的a,b,c等。


科目:高中數學 來源:2013屆廣東省高二文科數學競賽試卷(解析版) 題型:解答題
(本題滿分14分)
有甲乙兩個班級進行數學考試,按照大于等于85分為優秀,85分以下為非優秀統計成績后,得到如下的列聯表.
|
|
優秀 |
非優秀 |
總計 |
|
甲班 |
10 |
|
|
|
乙班 |
|
30 |
|
|
合計 |
|
|
105 |
已知在全部105人中抽到隨機抽取1人為優秀的概率為
(1)請完成上面的列聯表;
(2)根據列聯表的數據,若按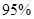 的可靠性要求,能否認為“成績與班級有關系” .
的可靠性要求,能否認為“成績與班級有關系” .
(3)若按下面的方法從甲班優秀的學生抽取一人:把甲班優秀的10名學生從2到11進行編號,先后兩次拋擲一枚均勻的骰子,出現的點數之和為被抽取人的序號.試求抽到6或10號的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
(本題滿分11分)設函數f (x)=![]() x3-
x3-![]() x2+ax.
x2+ax.
(Ⅰ)函數f (x)在(11, 2012)內單調遞減,求a范圍;
(Ⅱ) 若實數a滿足1<a≤2,函數g(x)=4x3+3bx2-6(b+2)x (b∈R) 的極小值點與f (x)的極小值點相同,求證:g(x)的極大值小于等于10.
查看答案和解析>>
科目:高中數學 來源: 題型:
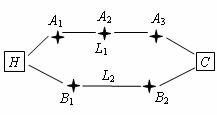
(本題滿分11分)張先生家住H小區,他在C科技園區工作,從家開車到公司上班有L1,L2兩條路線(如圖),L1路線上有A1,A2,A3三個路口,各路口遇到紅燈的概率均為![]() ;L2路線上有B1,B2兩個路口,各路口遇到紅燈的概率依次為
;L2路線上有B1,B2兩個路口,各路口遇到紅燈的概率依次為![]() ,
,![]() .
.
(Ⅰ)若走L1路線,求最多遇到1次紅燈的概率;
(Ⅱ)若走L2路線,求遇到紅燈次數![]() 的數學期望;
的數學期望;
(Ⅲ)按照“平均遇到紅燈次數最少”的要求,請你幫助張先生從上述兩條路線中選擇一條最好的上班路線,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
(本題滿分11分)從1到9的九個數字中取三個偶數三個奇數,組成沒有重復數字的6位數?試問:
(1)其中1在首位的有多少個?
(2)其中三個偶數字排在一起三個奇數字也排在一起的有多少個?
(3)其中任意兩偶然都不相鄰的六位數有多少個?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com