
(本題滿分12分)
設函數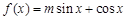
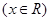 的圖象經過點
的圖象經過點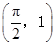 ,
,
(1)求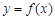 的解析式,并求函數的最小正周期和最大值;
的解析式,并求函數的最小正周期和最大值;
(2)如何由函數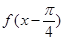 的圖象得到函數
的圖象得到函數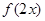 的圖象.
的圖象.
(1)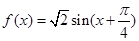 ,
, ,
,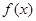 的最大值為
的最大值為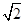 ;
;
(2)先把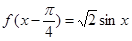 圖象上每一點向左平移
圖象上每一點向左平移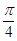 得到函數
得到函數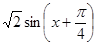 的圖象.再把函數
的圖象.再把函數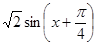 的圖象上任一點縱坐標不變,橫坐標變為原來的
的圖象上任一點縱坐標不變,橫坐標變為原來的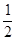 ,
,
得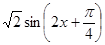
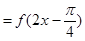 的圖象。
的圖象。
【解析】
試題分析:(Ⅰ) 函數
函數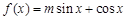
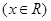 的圖象經過點
的圖象經過點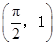
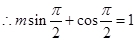
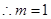 ………………2分
………………2分
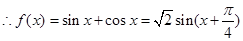 ……….4分
……….4分
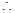 函數的最小正周期
函數的最小正周期 …………….5分
…………….5分
當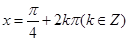 時,
時, 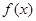 的最大值為
的最大值為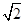 ,…………………….6分
,…………………….6分
(2)因為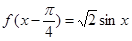
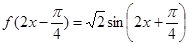 …………8分
…………8分
先把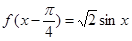 圖象上每一點向左平移
圖象上每一點向左平移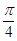 得到函數
得到函數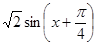 的圖象.10分
的圖象.10分
再把函數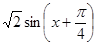 的圖象上任一點縱坐標不變,橫坐標變為原來的
的圖象上任一點縱坐標不變,橫坐標變為原來的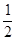 ,
,
得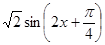
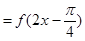 的圖象………………12分
的圖象………………12分
(可以先伸縮,后平移,相應得分)
考點:和差公式;周期公式;三角函數的變換。
點評:注意:把函數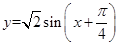 的圖象上任一點縱坐標不變,橫坐標變為原來的
的圖象上任一點縱坐標不變,橫坐標變為原來的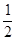 ,得到函數
,得到函數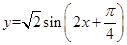 的圖像。而不是得到
的圖像。而不是得到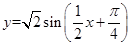 的圖像,此點容易出錯,一定要注意!
的圖像,此點容易出錯,一定要注意!


 孟建平小學滾動測試系列答案
孟建平小學滾動測試系列答案 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案科目:高中數學 來源: 題型:
| π | 2 |
查看答案和解析>>
科目:高中數學 來源:2012-2013學年上海市金山區高三上學期期末考試數學試卷(解析版) 題型:解答題
(本題滿分12分,第1小題6分,第2小題6分)
已知集合A={x| | x–a | < 2,xÎR
},B={x| <1,xÎR }.
<1,xÎR }.
(1) 求A、B;
(2) 若 ,求實數a的取值范圍.
,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年安徽省高三10月月考理科數學試卷(解析版) 題型:解答題
(本題滿分12分)
設函數 (
( ,
, 為常數),且方程
為常數),且方程 有兩個實根為
有兩個實根為 .
.
(1)求 的解析式;
的解析式;
(2)證明:曲線 的圖像是一個中心對稱圖形,并求其對稱中心.
的圖像是一個中心對稱圖形,并求其對稱中心.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年重慶市高三第二次月考文科數學 題型:解答題
(本題滿分12分,(Ⅰ)小問4分,(Ⅱ)小問6分,(Ⅲ)小問2分.)
如圖所示,直二面角 中,四邊形
中,四邊形 是邊長為
是邊長為 的正方形,
的正方形, ,
, 為
為 上的點,且
上的點,且 ⊥平面
⊥平面
(Ⅰ)求證: ⊥平面
⊥平面
(Ⅱ)求二面角 的大小;
的大小;
(Ⅲ)求點 到平面
到平面 的距離.
的距離.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com