
【題目】已知α是三角形的內角,且sinα+cosα= ![]() .
.
(1)求cos2α的值;
(2)把 ![]() 用tanα表示出來,并求其值.
用tanα表示出來,并求其值.
【答案】
(1)解:聯立得 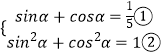 ,
,
由①得cosα= ![]() ﹣sinα,將其代入②,
﹣sinα,將其代入②,
整理得25sin2α﹣5sinα﹣12=0.
∵α是三角形內角,
∴可得:sinα= ![]() ,cosα=﹣
,cosα=﹣ ![]() .
.
cos2α=2cos2α﹣1=2× ![]() ﹣1=﹣
﹣1=﹣ ![]()
(2)解: ![]() =
= ![]() =
= ![]() ,
,
∵tanα=﹣ ![]() ,
,
∴ ![]() =
= ![]() =﹣
=﹣ ![]()
【解析】(1)聯立得 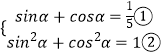 ,整理得25sin2α﹣5sinα﹣12=0,即可解得sinα,cosα的值,進而利用二倍角的余弦函數公式即可計算得解.(2)利用同角三角函數基本關系式可求
,整理得25sin2α﹣5sinα﹣12=0,即可解得sinα,cosα的值,進而利用二倍角的余弦函數公式即可計算得解.(2)利用同角三角函數基本關系式可求 ![]() =
= ![]() ,由(1)可求tanα=﹣
,由(1)可求tanα=﹣ ![]() ,即可計算得解.
,即可計算得解.
【考點精析】掌握同角三角函數基本關系的運用是解答本題的根本,需要知道同角三角函數的基本關系:![]()
![]() ;
;![]()
![]() ;(3) 倒數關系:
;(3) 倒數關系:![]() .
.


科目:高中數學 來源: 題型:
【題目】下列命題是真命題的是( )
A.a>b是ac2>bc2的充要條件
B.a>1,b>1是ab>1的充分條件
C.?x0∈R,e ![]() ≤0
≤0
D.若p∨q為真命題,則p∧q為真
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,點E,F分別為AB和PD中點. (Ⅰ)求證:直線AF∥平面PEC;
(Ⅱ)求PC與平面PAB所成角的正弦值.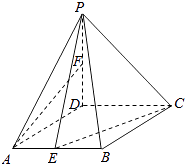
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是菱形,
是菱形, ![]() 平面
平面![]() ,
, ![]() 是棱
是棱![]() 上的一個動點.
上的一個動點.
(Ⅰ)若![]() 為
為![]() 的中點,求證:
的中點,求證: ![]() 平面
平面![]() ;
;
(Ⅱ)求證:平面![]() 平面
平面![]() ;
;
(Ⅲ)若三棱錐![]() 的體積是四棱錐
的體積是四棱錐![]() 體積的
體積的![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業有甲、乙兩個研發小組,他們研發新產品成功的概率分別為 ![]() 和
和 ![]() .現安排甲組研發新產品A,乙組研發新產品B,設甲、乙兩組的研發相互獨立. (Ⅰ)求至少有一種新產品研發成功的概率;
.現安排甲組研發新產品A,乙組研發新產品B,設甲、乙兩組的研發相互獨立. (Ⅰ)求至少有一種新產品研發成功的概率;
(Ⅱ)若新產品A研發成功,預計企業可獲利潤120萬元;若新產品B研發成功,預計企業可獲利潤100萬元,求該企業可獲利潤的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中常數
,其中常數![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 的單調遞增區間;
的單調遞增區間;
(2)當![]() 時,若函數
時,若函數![]() 有三個不同的零點,求
有三個不同的零點,求![]() 的取值范圍;
的取值范圍;
(3)設定義在![]() 上的函數
上的函數![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() ,當
,當![]() 時,若
時,若![]() 在
在![]() 內恒成立,則稱
內恒成立,則稱![]() 為函數
為函數![]() 的“類對稱點”,請你探究當
的“類對稱點”,請你探究當![]() 時,函數
時,函數![]() 是否存在“類對稱點”,若存在,請最少求出一個“類對稱點” 的橫坐標;若不存在,說明理由.
是否存在“類對稱點”,若存在,請最少求出一個“類對稱點” 的橫坐標;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com