
分析 設F(x)=f(x)-g(x),求出導函數,由x的范圍得到導函數值大雨0,即F(x)為增函數,根據閉區間x的范圍,求出F(x)的最大值,根據最大值大于0列出關于a的不等式,求出不等式的解集即可得到a的取值范圍.
解答 解:設F(x)=f(x)-g(x)=$\frac{1}{3}$a2x3-ax2+ax-$\frac{1}{3}$,(x∈(0,$\frac{1}{2}$]),
對F(x)求導,得F′(x)=a2x2-2ax+a=a2x2+a(1-2x)>0,(a>0),
∴F(x)在(0,$\frac{1}{2}$]上為增函數,則F(x)max=F($\frac{1}{2}$).
依題意,只需F(x)max>0,即$\frac{1}{3}$a2×$\frac{1}{8}$-a×$\frac{1}{4}$+a×$\frac{1}{2}$-$\frac{1}{3}$>0,
∴a2+6a-8>0,解得a>-3+$\sqrt{17}$或a<-3-$\sqrt{17}$(舍去).
于是,所求實數a的取值范圍是(-3+$\sqrt{17}$,+∞).
故答案為:(-3+$\sqrt{17}$,+∞).
點評 本題主要考查函數單調性的應用,根據條件構造函數,求函數的導數,利用函數的單調性和導數之間的關系進行轉化是解決本題的關鍵.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (x-1)2+y2=36 | B. | (x+1)2+y2=36 | C. | x2+(y+1)2=36 | D. | x2+(y-1)2=36 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
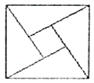 2002年8月,在北京召開的國際數學家大會會標如圖所示,它是由4個相同的直角三角形與中間的小正方形拼成的一大正方形,若直角三角形中較小的銳角為θ,大正方形的面積是25,小正方形的面積是1,則cos2θ的值等于( )
2002年8月,在北京召開的國際數學家大會會標如圖所示,它是由4個相同的直角三角形與中間的小正方形拼成的一大正方形,若直角三角形中較小的銳角為θ,大正方形的面積是25,小正方形的面積是1,則cos2θ的值等于( )| A. | 1 | B. | $-\frac{24}{25}$ | C. | $\frac{7}{25}$ | D. | -$\frac{7}{25}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | y=±$\frac{16}{9}x$ | B. | y=±$\frac{9}{16}$x | C. | y=±$\frac{3}{4}$x | D. | y=±$\frac{4}{3}$x |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com