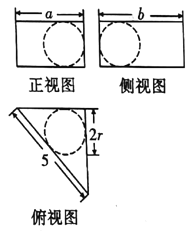
【題目】如圖是某組合體的三視圖，則內部幾何體的體積的最大值為（ ）
A. 
B. 
C. 
D. 
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】某商品在近30天內每件的銷售價格P（元）與時間t（天）的函數是：P=
該商品的日銷售量Q（件）與時間t（天）的函數關系是：Q=﹣t+40（0＜t≤30，t∈N*），求這種商品的日銷售金額的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=﹣x2+ax（a∈R）．
（1）當a=3時，求函數f（x）在[
,2]上的最大值和最小值；
（2）當函數f（x）在(,2)單調時，求a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】小型風力發電項目投資較少，開發前景廣闊.受風力自然資源影響，項目投資存在一定風險.根據測算，IEC（國際電工委員會）風能風區的分類標準如下：
風能分類 | 一類風區 | 二類風區 |
平均風速m/s | 8.5---10 | 6.5---8.5 |
某公司計劃用不超過100萬元的資金投資于A、B兩個小型風能發電項目.調研結果是：未來一年內，位于一類風區的A項目獲利
%的可能性為0.6，虧損
%的可能性為0.4；
B項目位于二類風區，獲利35%的可能性為0.6，虧損10%的可能性是0.2，不賠不賺的可能性是0.2.
假設投資A項目的資金為
（
）萬元，投資B項目資金為
（
）萬元，且公司要求對A項目的投資不得低于B項目.
（Ⅰ）記投資A，B項目的利潤分別為
和
，試寫出隨機變量
與
的分布列和期望
， 
;
（Ⅱ）根據以上的條件和市場調研，試估計一年后兩個項目的平均利潤之和
的最大值，并據此給出公司分配投資金額建議.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】求滿足下列條件的直線方程：
（1）求經過直線l1：x+3y﹣3=0，l2：x﹣y+1=0的交點，且平行于直線2x+y﹣3=0的直線l方程；
（2）求在兩坐標軸上截距相等，且與點A（3，1）的距離為
的直線l的方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】正方體ABCD﹣A1B1C1D1中，點M，N分別在線段AB1、BC1上，且AM=BN．以下結論：①AA1⊥MN；②A1C1∥MN；③MN∥平面A1B1C1D1；④MN與A1C1異面，⑤MN與 A1C1成30°．其中有可能成立的結論的個數為（ ）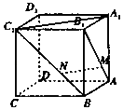 
A.5
B.4
C.3
D.2
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知半徑為2，圓心在直線y=x+2上的圓C．
（1）當圓C經過點A（2，2）且與y軸相切時，求圓C的方程；
（2）已知E（1，1），F（1，3），若圓C上存在點Q，使|QF|2﹣|QE|2=32，求圓心橫坐標a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】第96屆（春季）全國糖酒商品交易會于2017年3月23日至25日在四川舉辦.展館附近一家川菜特色餐廳為了研究參會人數與本店所需原材料數量的關系，在交易會前查閱了最近5次交易會的參會人數
（萬人）與餐廳所用原材料數量
（袋），得到如下數據：
（Ⅰ）請根據所給五組數據，求出
關于
的線性回歸方程
；
（Ⅱ）若該店現有原材料12袋，據悉本次交易會大約有13萬人參加，為了保證原材料能夠滿足需要，則該店應至少再補充原材料多少袋？
（參考公式： 
， 
）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
