
分析 (I)利用遞推關(guān)系即可得出.
(II)利用“錯(cuò)位相減法”與等比數(shù)列的求和公式即可得出.
解答 解:(Ⅰ)∵${S_n}={n^2}-2n$
∴n=1時(shí),a1=-1;n≥2時(shí),${a_n}={S_n}-{S_{n-1}}={n^2}-2n-{(n-1)^2}+2(n-1)=2n-3$
所以an=2n-3…6分
(Ⅱ)由(Ⅰ)知${b_n}=n•{2^{{a_n}+1}}=n•{2^{(2n-3)+1}}=n•{4^{n-1}}$…8分
${T_n}=1×{4^0}+2×{4^1}+3×{4^2}+…+n×{4^{n-1}}$…①
$4{T_n}=1×{4^1}+2×{4^2}+3×{4^3}+…+(n-1)×{4^{n-1}}+n×{4^n}$…②
①-②得:$-3{T_n}={4^0}+{4^1}+{4^2}+…+{4^{n-1}}-n×{4^n}$=$\frac{{1-{4^n}}}{1-4}-n×{4^n}=(\frac{1}{3}-n){4^n}-\frac{1}{3}$…11分
Tn=$\frac{{1-{4^n}}}{1-4}-n×{4^n}=\frac{3n-1}{9}•{4^n}+\frac{1}{9}$…12分.
點(diǎn)評(píng) 本題考查了數(shù)列遞推關(guān)系、等比數(shù)列的通項(xiàng)公式與求和公式、“錯(cuò)位相減法”,考查了推理能力與計(jì)算能力,屬于中檔題.


 互動(dòng)課堂系列答案
互動(dòng)課堂系列答案 激活思維智能訓(xùn)練課時(shí)導(dǎo)學(xué)練系列答案
激活思維智能訓(xùn)練課時(shí)導(dǎo)學(xué)練系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
 如圖,在四面體ABCD中,已知∠ABD=∠CBD=60°,AB=BC=2,CE⊥BD于E
如圖,在四面體ABCD中,已知∠ABD=∠CBD=60°,AB=BC=2,CE⊥BD于E查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 4π | B. | 8π | C. | 9π | D. | 36π |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 3x-4y+15=0 | B. | 3x+4y-33=0 | C. | 3x-4y+15=0或x=3 | D. | 3x+4y-33=0或x=3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | $\sqrt{3}$ | B. | 2 | C. | $\frac{\sqrt{17}}{3}$ | D. | $\frac{\sqrt{13}}{2}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
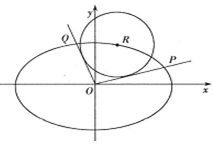 已知橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦點(diǎn)為F1(-$\sqrt{6}$,0),e=$\frac{\sqrt{2}}{2}$.
已知橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦點(diǎn)為F1(-$\sqrt{6}$,0),e=$\frac{\sqrt{2}}{2}$.查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com