
【題目】如圖,![]() 且
且![]() ,
,![]() ,
,![]() 且
且![]() ,
,![]() 且
且![]() ,
,![]() 平面
平面![]() ,
,![]() .
.
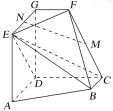
(1)若![]() 為
為![]() 的中點,
的中點,![]() 為
為![]() 的中點,求證:
的中點,求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值.
的正弦值.
科目:高中數學 來源: 題型:
【題目】將正方形ABCD沿對角線BD折成直二面角A-BD-C,有如下四個結論
①AC⊥BD;
②△ACD是等邊三角形;
③AB與平面BCD成60°的角;
④AB與CD所成的角是60°.
其中正確結論的序號是________
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了迎接2019年全國文明城市評比,某市文明辦對市民進行了一次文明創建知識的網絡問卷調查.每一位市民有且僅有一次參加機會,通過隨機抽樣,得到參加問卷調查的1000人的得分(滿分:100分)數據,統計結果如下表所示:
組別 |
|
|
|
|
|
|
|
頻數 | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
(1)由頻數分布表可以認為,此次問卷調查的得分![]() 服從正態分布
服從正態分布![]() ,
,![]() 近似為這1000人得分的平均值(同一組數據用該組區間的中點值作為代表),請利用正態分布的知識求
近似為這1000人得分的平均值(同一組數據用該組區間的中點值作為代表),請利用正態分布的知識求![]() ;
;
(2)在(1)的條件下,文明辦為此次參加問卷調查的市民制定如下獎勵方案:
(i)得分不低于![]() 的可以獲贈2次隨機話費,得分低于
的可以獲贈2次隨機話費,得分低于![]() 的可以獲贈1次隨機話費;
的可以獲贈1次隨機話費;
(ii)每次獲贈的隨機話費和對應的概率為:
獲贈的隨機話費(單位:元) | 20 | 40 |
概率 |
|
|
現市民小王要參加此次問卷調查,記![]() (單位:元)為該市民參加問卷調查獲贈的話費,求
(單位:元)為該市民參加問卷調查獲贈的話費,求![]() 的分布列及數學期望.
的分布列及數學期望.
附:①![]() ;
;
②若![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廠銷售部以箱為單位銷售某種零件,每箱的定價為![]() 元,低于
元,低于![]() 箱按原價銷售,不低于
箱按原價銷售,不低于![]() 箱則有以下兩種優惠方案:①以
箱則有以下兩種優惠方案:①以![]() 箱為基準,每多
箱為基準,每多![]() 箱送
箱送![]() 箱;②通過雙方議價,買方能以優惠
箱;②通過雙方議價,買方能以優惠![]() 成交的概率為
成交的概率為![]() ,以優惠
,以優惠![]() 成交的概率為
成交的概率為![]() .
.
![]() 甲、乙兩單位都要在該廠購買
甲、乙兩單位都要在該廠購買![]() 箱這種零件,兩單位都選擇方案②,且各自達成的成交價格相互獨立,求甲單位優惠比例不低于乙單位優惠比例的概率;
箱這種零件,兩單位都選擇方案②,且各自達成的成交價格相互獨立,求甲單位優惠比例不低于乙單位優惠比例的概率;
![]() 某單位需要這種零件
某單位需要這種零件![]() 箱,以購買總價的數學期望為決策依據,試問該單位選擇哪種優惠方案更劃算?
箱,以購買總價的數學期望為決策依據,試問該單位選擇哪種優惠方案更劃算?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系,直線
軸正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程和直線
的普通方程和直線![]() 的直角坐標方程;
的直角坐標方程;
(2)射線![]() 的極坐標方程為
的極坐標方程為![]() ,若射線
,若射線![]() 與曲線
與曲線![]() 的交點為
的交點為![]() ,與直線
,與直線![]() 的交點為
的交點為![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com