
【題目】已知點![]() 是拋物線
是拋物線![]() :
:![]() 的焦點,點
的焦點,點![]() 為拋物線
為拋物線![]() 的對稱軸與其準線的交點,過
的對稱軸與其準線的交點,過![]() 作拋物線
作拋物線![]() 的切線,切點為
的切線,切點為![]() ,若點
,若點![]() 恰好在以
恰好在以![]() ,
,![]() 為焦點的雙曲線上,則雙曲線的離心率為( )
為焦點的雙曲線上,則雙曲線的離心率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中數學 來源: 題型:
【題目】某調查機構對全國互聯網行業進行調查統計,得到整個互聯網行業從業者年齡分布餅狀圖,90后從事互聯網行業崗位分布條形圖,則下列結論中不正確的是( )
注:90后指1990年及以后出生,80后指1980-1989年之間出生,80前指1979年及以前出生.


A.互聯網行業從業人員中90后占一半以上
B.互聯網行業中從事技術崗位的人數超過總人數的![]()
C.互聯網行業中從事運營崗位的人數90后比80前多
D.互聯網行業中從事技術崗位的人數90后比80后多
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我市某區2018年房地產價格因“棚戶區改造”實行貨幣化補償,使房價快速走高,為抑制房價過快上漲,政府從2019年2月開始采用實物補償方式(以房換房),3月份開始房價得到很好的抑制,房價漸漸回落,以下是2019年2月后該區新建住宅銷售均價的數據:
月份 | 3 | 4 | 5 | 6 | 7 |
價格 | 83 | 82 | 80 | 78 | 77 |
(1)研究發現,3月至7月的各月均價![]() (百元/平方米)與月份
(百元/平方米)與月份![]() 之間具有較強的線性相關關系,求價格
之間具有較強的線性相關關系,求價格![]() (百元/平方米)關于月份
(百元/平方米)關于月份![]() 的線性回歸方程;
的線性回歸方程;
(2)用![]() 表示用(1)中所求的線性回歸方程得到的與
表示用(1)中所求的線性回歸方程得到的與![]() 對應的銷售均價的估計值,3月份至7月份銷售均價估計值
對應的銷售均價的估計值,3月份至7月份銷售均價估計值![]() 與實際相應月份銷售均價
與實際相應月份銷售均價![]() 差的絕對值記為
差的絕對值記為![]() ,即
,即![]() ,
,![]() .若
.若![]() ,則將銷售均價的數據
,則將銷售均價的數據稱為一個“好數據”,現從5個銷售均價數據中任取2個,求抽取的2個數據均是“好數據”的概率.
參考公式:回歸方程系數公式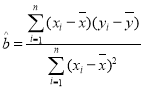 ,
,![]() ;參考數據:
;參考數據:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學生為了測試煤氣灶燒水如何節省煤氣的問題設計了一個實驗,并獲得了煤氣開關旋鈕旋轉的弧度數![]() 與燒開一壺水所用時間
與燒開一壺水所用時間![]() 的一組數據,且作了一定的數據處理(如下表),得到了散點圖(如下圖).
的一組數據,且作了一定的數據處理(如下表),得到了散點圖(如下圖).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.

(1)根據散點圖判斷,![]() 與
與![]() 哪一個更適宜作燒水時間
哪一個更適宜作燒水時間![]() 關于開關旋鈕旋轉的弧度數
關于開關旋鈕旋轉的弧度數![]() 的回歸方程類型?(不必說明理由)
的回歸方程類型?(不必說明理由)
(2)根據判斷結果和表中數據,建立![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(3)若單位時間內煤氣輸出量![]() 與旋轉的弧度數
與旋轉的弧度數![]() 成正比,那么,利用第(2)問求得的回歸方程知
成正比,那么,利用第(2)問求得的回歸方程知![]() 為多少時,燒開一壺水最省煤氣?
為多少時,燒開一壺水最省煤氣?
附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘法估計值分別為
的斜率和截距的最小二乘法估計值分別為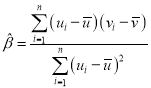 ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于數列![]() ,若從第二項起的每一項均大于該項之前的所有項的和,則稱
,若從第二項起的每一項均大于該項之前的所有項的和,則稱![]() 為
為![]() 數列.
數列.
(1)若![]() 的前
的前![]() 項和
項和![]() ,試判斷
,試判斷![]() 是否是
是否是![]() 數列,并說明理由;
數列,并說明理由;
(2)設數列![]() 是首項為
是首項為![]() 、公差為
、公差為![]() 的等差數列,若該數列是
的等差數列,若該數列是![]() 數列,求
數列,求![]() 的取值范圍;
的取值范圍;
(3)設無窮數列![]() 是首項為
是首項為![]() 、公比為
、公比為![]() 的等比數列,有窮數列
的等比數列,有窮數列![]() ,
,![]() 是從
是從![]() 中取出部分項按原來的順序所組成的不同數列,其所有項和分別為
中取出部分項按原來的順序所組成的不同數列,其所有項和分別為![]() ,
,![]() ,求
,求![]() 是
是![]() 數列時
數列時![]() 與
與![]() 所滿足的條件,并證明命題“若
所滿足的條件,并證明命題“若![]() 且
且![]() ,則
,則![]() 不是
不是![]() 數列”.
數列”.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】手工藝是一種生活態度和對傳統的堅持,在我國有很多手工藝品制作村落,村民的手工技藝世代相傳,有些村落制造出的手工藝品不僅全國聞名,還大量遠銷海外.近年來某手工藝品村制作的手工藝品在國外備受歡迎,該村村民成立了手工藝品外銷合作社,為嚴把質量關,合作社對村民制作的每件手工藝品都請3位行家進行質量把關,質量把關程序如下:(i)若一件手工藝品3位行家都認為質量過關,則該手工藝品質量為A級;(ii)若僅有1位行家認為質量不過關,再由另外2位行家進行第二次質量把關,若第二次質量把關這2位行家都認為質量過關,則該手工藝品質量為B級,若第二次質量把關這2位行家中有1位或2位認為質量不過關,則該手工藝品質量為C級;(iii)若有2位或3位行家認為質量不過關,則該手工藝品質量為D級.已知每一次質量把關中一件手工藝品被1位行家認為質量不過關的概率為![]() ,且各手工藝品質量是否過關相互獨立.
,且各手工藝品質量是否過關相互獨立.
(1)求一件手工藝品質量為B級的概率;
(2)若一件手工藝品質量為A,B,C級均可外銷,且利潤分別為900元,600元,300元,質量為D級不能外銷,利潤記為100元.
①求10件手工藝品中不能外銷的手工藝品最有可能是多少件;
②記1件手工藝品的利潤為X元,求X的分布列與期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() 平面
平面![]() ,四邊形
,四邊形![]() 為正方形,點
為正方形,點![]() 為線段
為線段![]() 上的點,過
上的點,過![]() 三點的平面與
三點的平面與![]() 交于點
交于點![]() .將①
.將①![]() ,②
,②![]() ,③
,③![]() 中的兩個補充到已知條件中,解答下列問題:
中的兩個補充到已知條件中,解答下列問題:
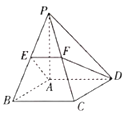
(1)求平面![]() 將四棱錐分成兩部分的體積比;
將四棱錐分成兩部分的體積比;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() .
.
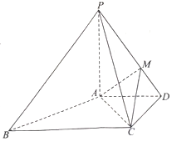
(1)證明:![]() 平面
平面![]() ;
;
(2)在線段![]() 上,是否存在一點
上,是否存在一點![]() ,使得二面角
,使得二面角![]() 的大小為
的大小為![]() ?如果存在,求
?如果存在,求![]() 的值;如果不存在,請說明理由.
的值;如果不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 過點
過點![]() 且橢圓的短軸長為
且橢圓的短軸長為![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)已知動直線![]() 過右焦點
過右焦點![]() ,且與橢圓
,且與橢圓![]() 分別交于
分別交于![]() 兩點.試問
兩點.試問![]() 軸上是否存在定點
軸上是否存在定點![]() ,使得,
,使得,![]() 恒成立?若存在求出點
恒成立?若存在求出點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com