
【題目】設橢圓![]() (
(![]() )的右焦點為
)的右焦點為![]() ,右頂點為
,右頂點為![]() ,已知
,已知![]() ,其中
,其中![]() 為原點,
為原點,![]() 為橢圓的離心率.
為橢圓的離心率.
(Ⅰ)求橢圓的方程;
(Ⅱ)設過點![]() 的直線
的直線![]() 與橢圓交于點
與橢圓交于點![]() (
(![]() 不在
不在![]() 軸上),垂直于
軸上),垂直于![]() 的直線與
的直線與![]() 交于點
交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,若
,若![]() ,且
,且![]() ,求直線的
,求直線的![]() 斜率.
斜率.
 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=xlnx的圖象上有A、B兩點,其橫坐標為x1 , x2(0<x1<x2<1)且滿足f(x1)=f(x2),若k=5( ![]() +
+ ![]() ),且k為整數時,則k的值為( )(參考數據:e≈2.72)
),且k為整數時,則k的值為( )(參考數據:e≈2.72)
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-5:不等式選講
已知函數f(x)=|x﹣a|+|x+5﹣a|
(1)若不等式f(x)﹣|x﹣a|≤2的解集為[﹣5,﹣1],求實數a的值;
(2)若x0∈R,使得f(x0)<4m+m2 , 求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】兩縣城A和B相距20km,現計劃在兩縣城外以AB為直徑的半圓弧上選擇一點C建造垃圾處理廠,其對城市的影響度與所選地點到城市的距離有關,對城A和城B的總影響度為城A與城B的影響度之和,記C點到城A的距離為xkm,建在C處的垃圾處理廠對城A和城B的總影響度為y,統計調查表明:垃圾處理廠對城A的影響度與所選地點到城A的距離的平方成反比,比例系數為4;對城B的影響度與所選地點到城B的距離的平方成反比,比例系數為k,當垃圾處理廠建在的 ![]() 中點時,對城A和城B的總影響度為0.065.
中點時,對城A和城B的總影響度為0.065. 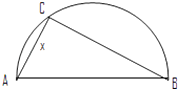
(1)將y表示成x的函數;
(2)討論(1)中函數的單調性,并判斷弧 ![]() 上是否存在一點,使建在此處的垃圾處理廠對城A和城B的總影響度最小?若存在,求出該點到城A的距離;若不存在,說明理由.
上是否存在一點,使建在此處的垃圾處理廠對城A和城B的總影響度最小?若存在,求出該點到城A的距離;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列幾個命題:
①命題p:任意x∈R,都有cosx≤1,則¬p:存在x0∈R,使得cosx0≤1
②命題“若a>2且b>2,則a+b>4且ab>4”的逆命題為假命題
③空間任意一點O和三點A,B,C,則 ![]() =3
=3 ![]() =2
=2 ![]() 是A,B,C三點共線的充分不必要條件
是A,B,C三點共線的充分不必要條件
④線性回歸方程y=bx+a對應的直線一定經過其樣本數據點(x1 , y1),(x2 , y2),…,(xn , yn)中的一個
其中不正確的個數為( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知A,B是橢圓 ![]() =1和雙曲線
=1和雙曲線 ![]() =1的公共頂點,其中a>b>0,P是雙曲線上的動點,M是橢圓上的動點(P,M都異于A,B),且滿足
=1的公共頂點,其中a>b>0,P是雙曲線上的動點,M是橢圓上的動點(P,M都異于A,B),且滿足 ![]() =λ(
=λ( ![]() )(λ∈R),設直線AP,BP,AM,BM的斜率分別為k1 , k2 , k3 , k4 , 若k1+k2=
)(λ∈R),設直線AP,BP,AM,BM的斜率分別為k1 , k2 , k3 , k4 , 若k1+k2= ![]() ,則k3+k4= .
,則k3+k4= .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】目前,學案導學模式已經成為教學中不可或缺的一部分,為了了解學案的合理使用是否對學生的期末復習有著重要的影響,我校隨機抽取100名學生,對學習成績和學案使用程度進行了調查,統計數據如表所示:
善于使用學案 | 不善于使用學案 | 總計 | |
學習成績優秀 | 40 | ||
學習成績一般 | 30 | ||
總計 | 100 |
參考公式: ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
參考數據:
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
已知隨機抽查這100名學生中的一名學生,抽到善于使用學案的學生概率是0.6.
(1)請將上表補充完整(不用寫計算過程);
(2)試運用獨立性檢驗的思想方法分析:有多大的把握認為學生的學習成績與對待學案的使用態度有關?
(3)利用分層抽樣的方法從善于使用學案的同學中隨機抽取6人,從這6人中抽出3人繼續調查,設抽出學習成績優秀的人數為X,求X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在極坐標系中,圓![]() 的方程為
的方程為![]() ,以坐標原點為極點,
,以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,直線
軸正半軸為極軸建立極坐標系,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數)
為參數)
(1)求圓![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的普通方程;
的普通方程;
(2)若直線![]() 與圓
與圓![]() 相切,求實數
相切,求實數![]() 的值;
的值;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com