
【題目】新高考方案規定,普通高中學業水平考試分為合格性考試(合格考)和選擇性考試(選擇考).其中“選擇考”成績將計入高考總成績,即“選擇考”成績根據學生考試時的原始卷面分數,由高到低進行排序,評定為![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五個等級.某試點高中2018年參加“選擇考”總人數是2016年參加“選擇考”總人數的2倍,為了更好地分析該校學生“選擇考”的水平情況,統計了該校2016年和2018年“選擇考”成績等級結果,得到如下圖表:
五個等級.某試點高中2018年參加“選擇考”總人數是2016年參加“選擇考”總人數的2倍,為了更好地分析該校學生“選擇考”的水平情況,統計了該校2016年和2018年“選擇考”成績等級結果,得到如下圖表:
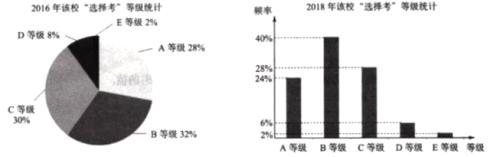
針對該校“選擇考”情況,2018年與2016年比較,下列說法正確的是( )
A. 獲得A等級的人數減少了B. 獲得B等級的人數增加了1.5倍
C. 獲得D等級的人數減少了一半D. 獲得E等級的人數相同
 英語小英雄天天默寫系列答案
英語小英雄天天默寫系列答案 暑假作業安徽少年兒童出版社系列答案
暑假作業安徽少年兒童出版社系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,已知曲線![]() 上的動點
上的動點![]() 到點
到點![]() 的距離與到直線
的距離與到直線![]() 的距離相等.
的距離相等.
(1)求曲線![]() 的軌跡方程;
的軌跡方程;
(2)過點![]() 分別作射線
分別作射線![]() 、
、![]() 交曲線
交曲線![]() 于不同的兩點
于不同的兩點![]() 、
、![]() ,且
,且![]() .試探究直線
.試探究直線![]() 是否過定點?如果是,請求出該定點;如果不是,請說明理由.
是否過定點?如果是,請求出該定點;如果不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】唐三彩,中國古代陶瓷燒制工藝的珍品,它吸取了中國國畫、雕塑等工藝美術的特點,在中國文化中占有重要的歷史地位,在中國的陶瓷史上留下了濃墨重彩的一筆.唐三彩的生產至今已有![]() 多年的歷史,對唐三彩的復制和仿制工藝,至今也有百余年的歷史.某陶瓷廠在生產過程中,對仿制的
多年的歷史,對唐三彩的復制和仿制工藝,至今也有百余年的歷史.某陶瓷廠在生產過程中,對仿制的![]() 件工藝品測得重量(單位:
件工藝品測得重量(單位:![]() )數據如下表:
)數據如下表:
分組 | 頻數 | 頻率 |
|
|
|
|
| |
|
| |
|
|
|
|
| |
|
| |
合計 |
|
(1)求出頻率分布表中實數![]() ,
,![]() 的值;
的值;
(2)若從仿制的![]() 件工藝品重量范圍在
件工藝品重量范圍在![]() 的工藝品中隨機抽選
的工藝品中隨機抽選![]() 件,求被抽選
件,求被抽選![]() 件工藝品重量均在范圍
件工藝品重量均在范圍![]() 中的概率.
中的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列敘述正確的是( )
A.命題“p且q”為真,則![]() 恰有一個為真命題
恰有一個為真命題
B.命題“已知![]() ,則“
,則“![]() ”是“
”是“![]() ”的充分不必要條件”
”的充分不必要條件”
C.命題![]() 都有
都有![]() ,則
,則![]() ,使得
,使得![]()
D.如果函數![]() 在區間
在區間![]() 上是連續不斷的一條曲線,并且有
上是連續不斷的一條曲線,并且有![]() ,那么函數
,那么函數![]() 在區間
在區間![]() 內有零點
內有零點
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】武漢有“九省通衢”之稱,也稱為“江城”,是國家歷史文化名城.其中著名的景點有黃鶴樓、戶部巷、東湖風景區等等.
(1)為了解“五·一”勞動節當日江城某旅游景點游客年齡的分布情況,從年齡在22歲到52歲的游客中隨機抽取了1000人,制成了如圖的頻率分布直方圖:
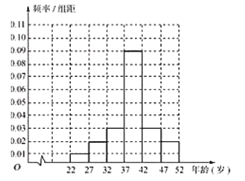
現從年齡在![]() 內的游客中,采用分層抽樣的方法抽取10人,再從抽取的10人中隨機抽取4人,記4人中年齡在
內的游客中,采用分層抽樣的方法抽取10人,再從抽取的10人中隨機抽取4人,記4人中年齡在![]() 內的人數為
內的人數為![]() ,求
,求![]() ;
;
(2)為了給游客提供更舒適的旅游體驗,該旅游景點游船中心計劃在2020年勞動節當日投入至少1艘至多3艘![]() 型游船供游客乘坐觀光.由2010到2019這10年間的數據資料顯示每年勞動節當日客流量
型游船供游客乘坐觀光.由2010到2019這10年間的數據資料顯示每年勞動節當日客流量![]() (單位:萬人)都大于1.將每年勞動節當日客流量數據分成3個區間整理得表:
(單位:萬人)都大于1.將每年勞動節當日客流量數據分成3個區間整理得表:
勞動節當日客流量 |
|
|
|
頻數(年) | 2 | 4 | 4 |
以這10年的數據資料記錄的3個區間客流量的頻率作為每年客流量在該區間段發生的概率,且每年勞動節當日客流量相互獨立.
該游船中心希望投入的![]() 型游船盡可能被充分利用,但每年勞動節當日
型游船盡可能被充分利用,但每年勞動節當日![]() 型游船最多使用量(單位:艘)要受當日客流量
型游船最多使用量(單位:艘)要受當日客流量![]() (單位:萬人)的影響,其關聯關系如下表:
(單位:萬人)的影響,其關聯關系如下表:
勞動節當日客流量 |
|
|
|
| 1 | 2 | 3 |
若某艘![]() 型游船在勞動節當日被投入且被使用,則游船中心當日可獲得利潤3萬元;若某艘
型游船在勞動節當日被投入且被使用,則游船中心當日可獲得利潤3萬元;若某艘![]() 型游船勞動節當日被投入卻不被使用,則游船中心當日虧損0.5萬元.記
型游船勞動節當日被投入卻不被使用,則游船中心當日虧損0.5萬元.記![]() (單位:萬元)表示該游船中心在勞動節當日獲得的總利潤,
(單位:萬元)表示該游船中心在勞動節當日獲得的總利潤,![]() 的數學期望越大游船中心在勞動節當日獲得的總利潤越大,問該游船中心在2020年勞動節當日應投入多少艘
的數學期望越大游船中心在勞動節當日獲得的總利潤越大,問該游船中心在2020年勞動節當日應投入多少艘![]() 型游船才能使其當日獲得的總利潤最大?
型游船才能使其當日獲得的總利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】焦點在![]() 軸上的橢圓
軸上的橢圓![]() 經過點
經過點![]() ,橢圓
,橢圓![]() 的離心率為
的離心率為![]() .
.![]() ,
,![]() 是橢圓的左、右焦點,
是橢圓的左、右焦點,![]() 為橢圓上任意點.
為橢圓上任意點.
(1)若![]() 面積為
面積為![]() ,求
,求![]() 的值;
的值;
(2)若點![]() 為
為![]() 的中點(
的中點(![]() 為坐標原點),過
為坐標原點),過![]() 且平行于
且平行于![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,是否存在實數
兩點,是否存在實數![]() ,使得
,使得![]() ;若存在,請求出
;若存在,請求出![]() 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com