
【題目】如圖:邊長為![]() 的菱形
的菱形![]() ,
,![]() ,將
,將![]() 沿
沿![]() 折起到圖中
折起到圖中![]() 的位置,使得二面角
的位置,使得二面角![]() 的大小為
的大小為![]() ,則三棱錐
,則三棱錐![]() 的外接球表面積等于_______.
的外接球表面積等于_______.

【答案】![]() .
.
【解析】
由題意取BD中點M,則∠DAB=60°為二面角P﹣BD﹣C的平面角,△PMC是邊長為3的正三角形,E,F分別為PM,CM靠近M的三等分點,作EO⊥面PBD,FO⊥面BCD,則O為外接球球心.利用球心到各頂點距離相等構造直角三角形求解外接球的半徑R,可得答案.
由題意,如圖:取BD中點M,
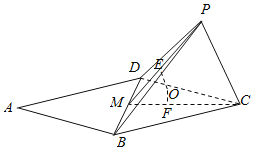
則∠DAB=60°為二面角P﹣BD﹣C的平面角,
△PMC是邊長為3的正三角形,E,F分別為PM,CM靠近M的三等分點,
作EO⊥面PBD,FO⊥面BCD,則O為外接球球心.
∵MF=1,PMC=60°,連接OC,OM,可得∠OMC=30°,
∴OF=![]() MO
MO
∴OF=![]()
∵FC=2
∴R2=OF2+FC2=![]()
三棱錐P﹣BCD的外接球表面積S=4πR2=![]()
故答案為:![]() .
.


科目:高中數學 來源: 題型:
【題目】下列命題中正確命題的個數是
(1)對分類變量![]() 與
與![]() 的隨機變量
的隨機變量![]() 的觀測值
的觀測值![]() 來說,
來說,![]() 越小,判斷“
越小,判斷“![]() 與
與![]() 有關系”的把握越大;
有關系”的把握越大;
(2)若將一組樣本數據中的每個數據都加上同一個常數后,則樣本的方差不變;
(3)在殘差圖,殘差點分布的帶狀區域的寬度越狹窄,其模型擬合的精度越高;
(4)設隨機變量![]() 服從正態分布
服從正態分布![]() ;
;
若![]() ,則
,則![]() ( )
( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年2月9-25日,第23屆冬奧會在韓國平昌舉行.4年后,第24屆冬奧會將在中國北京和張家口舉行.為了宣傳冬奧會,某大學在平昌冬奧會開幕后的第二天,從全校學生中隨機抽取了120名學生,對是否收看平昌冬奧會開幕式情況進行了問卷調查,統計數據如下:
收看 | 沒收看 | |
男生 | 60 | 20 |
女生 | 20 | 20 |
(Ⅰ)根據上表說明,能否有![]() 的把握認為,收看開幕式與性別有關?
的把握認為,收看開幕式與性別有關?
(Ⅱ)現從參與問卷調查且收看了開幕式的學生中,采用按性別分層抽樣的方法選取8人,參加2022年北京冬奧會志愿者宣傳活動.
(ⅰ)問男、女學生各選取多少人?
(ⅱ)若從這8人中隨機選取2人到校廣播站開展冬奧會及冰雪項目宣傳介紹,求恰好選到一名男生一名女生的概率P.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,點
,點![]() 也為拋物線
也為拋物線![]() 的焦點.(1)若
的焦點.(1)若![]() 為橢圓
為橢圓![]() 上兩點,且線段
上兩點,且線段![]() 的中點為
的中點為![]() ,求直線
,求直線![]() 的斜率;
的斜率;
(2)若過橢圓![]() 的右焦點
的右焦點![]() 作兩條互相垂直的直線分別交橢圓于
作兩條互相垂直的直線分別交橢圓于![]() 和
和![]() ,設線段
,設線段![]() 的長分別為
的長分別為![]() ,證明
,證明![]() 是定值.
是定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的導函數為
的導函數為![]() ,且對任意的實數
,且對任意的實數![]() 都有
都有![]() (
(![]() 是自然對數的底數),且
是自然對數的底數),且![]() ,若關于
,若關于![]() 的不等式
的不等式![]() 的解集中恰有兩個整數,則實數
的解集中恰有兩個整數,則實數![]() 的取值范圍是
的取值范圍是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】醫藥公司針對某種疾病開發了一種新型藥物,患者單次服用制定規格的該藥物后,其體內的藥物濃度![]() 隨時間
隨時間![]() 的變化情況(如圖所示):當
的變化情況(如圖所示):當![]() 時,
時,![]() 與
與![]() 的函數關系式為
的函數關系式為![]() (
(![]() 為常數);當
為常數);當![]() 時,
時,![]() 與
與![]() 的函數關系式為
的函數關系式為![]() (
(![]() 為常數).服藥
為常數).服藥![]() 后,患者體內的藥物濃度為
后,患者體內的藥物濃度為![]() ,這種藥物在患者體內的藥物濃度不低于最低有效濃度,才有療效;而超過最低中毒濃度,患者就會有危險.
,這種藥物在患者體內的藥物濃度不低于最低有效濃度,才有療效;而超過最低中毒濃度,患者就會有危險.
(1)首次服藥后,藥物有療效的時間是多長?
(2)首次服藥1小時后,可否立即再次服用同種規格的這種藥物?
(參考數據:![]() ,
,![]() )
)

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將圓![]() 上每一點的橫坐標變為原來的2倍,縱坐標變為原來的4倍,得曲線
上每一點的橫坐標變為原來的2倍,縱坐標變為原來的4倍,得曲線![]() .
.
(1)寫出![]() 的參數方程;
的參數方程;
(2)設直線![]() 與
與![]() 的交點為
的交點為![]() ,以坐標原點為極點,
,以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,求過線段
軸正半軸為極軸建立極坐標系,求過線段![]() 的中點與
的中點與![]() 垂直的直線的極坐標方程.
垂直的直線的極坐標方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)=|lnx|,若函數g(x)=f(x)-ax在區間(0,4)上有三個零點,則實數a的取值范圍是( )
A. (0,![]() )B. (
)B. (![]() ,e)C. (
,e)C. (![]() ,
,![]() )D. (0,
)D. (0,![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com