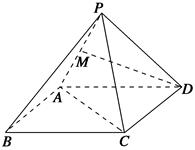
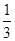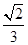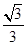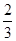已知正四棱錐
P-ABCD的側棱與底面所成角為60°,
M為
PA中點,連接
DM,則
DM與平面
PAC所成角的大小是________.
設底面正方形的邊長為
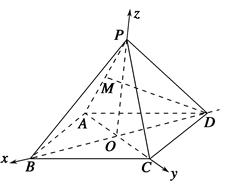
a,由已知可得正四棱錐的高為
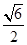 a
a,建立如圖所示空間直角坐標系,
則平面
PAC的法向量為
n=(1,0,0),
D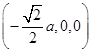
,
A0,-
 a
a,0,
P
,
M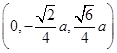
,

=
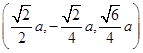
,所以cos 〈

,
n〉=
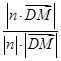
=

,所以
DM與平面
PAC所成角為45°.
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,平面

平面

,四邊形

為矩形,

.

為

的中點,

.

(1)求證:

;
(2)若

時,求二面角

的余弦值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,在四棱錐
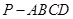
中,底面
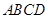
是邊長為1的菱形,
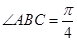
,
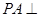
底面
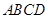
,
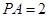
,
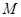
為
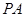
的中點,
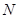
為
的中點,
于
,如圖建立空間直角坐標系.
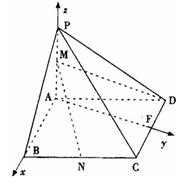
(1)求出平面
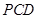
的一個法向量并證明
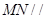
平面
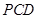
;
(2)求二面角
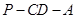
的余弦值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
在如圖所示的幾何體中,四邊形ABCD為正方形,
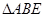
為等腰直角三角形,
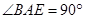
,且
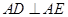
.
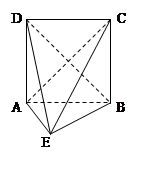
(1)證明:平面
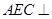
平面
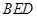
.
(2)求直線EC與平面BED所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,在直四棱柱
ABCD-A1B1C1D1中,底面
ABCD為等腰梯形,
AB∥
CD,
AB=4,
BC=
CD=2,
AA1=2,
E,
E1,
F分別是棱
AD,
AA1,
AB的中點.
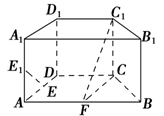
(1)證明:直線
EE1∥平面
FCC1;
(2)求二面角
B-FC1-
C的余弦值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
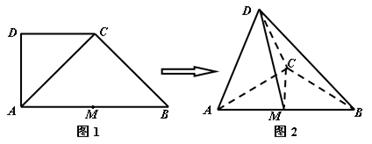
如圖1, 在直角梯形
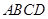
中,
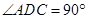
,
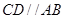
,
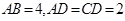
,
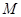
為線段
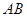
的中點. 將
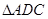
沿
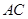
折起,使平面
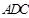
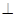
平面
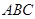
,得到幾何體
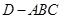
,如圖2所示.
(1)求證:
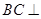
平面
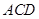
;
(2)求二面角
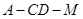
的余弦值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
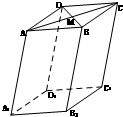
如圖,在底面ABCD為平行四邊形的四棱柱ABCD-A
1B
1C
1D
1中,M是AC與BD的交點,若
=,=,=,則下列向量中與
相等的向量是( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知三棱柱
ABC-
A1B1C1的側棱與底面邊長都相等,
A1在底面
ABC內的射影為△
ABC的中心,則
AB1與底面
ABC所成角的正弦值等于( ).
查看答案和解析>>


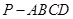 中,底面
中,底面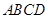 是邊長為1的菱形,
是邊長為1的菱形,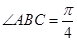 ,
,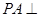 底面
底面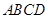 ,
,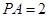 ,
,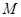 為
為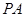 的中點,
的中點,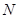 為
為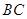 的中點,
的中點,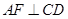 于
于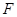 ,如圖建立空間直角坐標系.
,如圖建立空間直角坐標系.
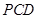 的一個法向量并證明
的一個法向量并證明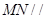 平面
平面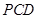 ;
;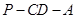 的余弦值.
的余弦值.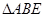 為等腰直角三角形,
為等腰直角三角形,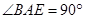 ,且
,且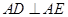 .
.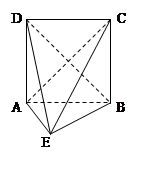
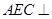 平面
平面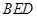 .
.
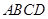 中,
中, 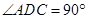 ,
, 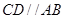 ,
,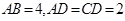 ,
,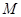 為線段
為線段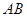 的中點. 將
的中點. 將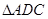 沿
沿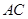 折起,使平面
折起,使平面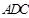
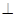 平面
平面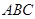 ,得到幾何體
,得到幾何體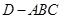 ,如圖2所示.
,如圖2所示.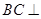 平面
平面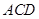 ;
; 的余弦值.
的余弦值.