
已知直線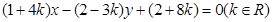 所經過的定點F,直線
所經過的定點F,直線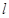 :
: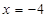 與x軸的交點是圓C的圓心,圓C恰好經過坐標原點O,設G是圓C上任意一點.
與x軸的交點是圓C的圓心,圓C恰好經過坐標原點O,設G是圓C上任意一點.
(1)求點F和圓C的方程;
(2)若直線FG與直線 交于點T,且G為線段FT的中點,求直線FG被圓C所截得的弦長;
交于點T,且G為線段FT的中點,求直線FG被圓C所截得的弦長;
(3)在平面上是否存在一點P,使得 ?若存在,求出點P坐標;若不存在,請說明理由.
?若存在,求出點P坐標;若不存在,請說明理由.
解(1)(1)由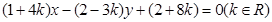 ,得
,得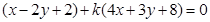 ,
,
則由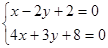 ,解得
,解得 …………………2分
…………………2分
,得 :
: ,
, ,
,
又圓C過原點,所以圓C的方程為 .………………………………4分
.………………………………4分
(2)由題意,得 ,代入
,代入 ,得
,得 ,
,
所以 的斜率為
的斜率為 ,
, 的方程為
的方程為 , …………………8分
, …………………8分
(注意:若點G或FG方程只寫一種情況扣1分)
所以 到
到 的距離為
的距離為 ,直線
,直線 被圓C截得弦長為
被圓C截得弦長為 .
.
故直線 被圓C截得弦長為7.…………………………………………………………10分
被圓C截得弦長為7.…………………………………………………………10分
(3)設 ,
, ,則由
,則由 ,得
,得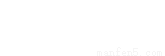 ,
,
整理得 ①,…………………………12分
①,…………………………12分
又 在圓C:
在圓C: 上,所以
上,所以 ②,
②,
②代入①得 , …………………………14分
, …………………………14分
又由 為圓C 上任意一點可知,
為圓C 上任意一點可知, 解得
解得 .
.
所以在平面上存在一點P,其坐標為 . …………………………16分
. …………………………16分
【解析】略


科目:高中數學 來源: 題型:
(09年濱州一模文)(14分)
已知直線![]() 所經過的定點
所經過的定點![]() 恰好是橢圓
恰好是橢圓![]() 的一個焦點,且橢圓
的一個焦點,且橢圓![]() 上的點到點
上的點到點![]() 的最大距離為8.
的最大距離為8.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)已知圓![]() ,直線
,直線![]() .試證明:當點
.試證明:當點![]() 在橢圓
在橢圓![]() 上運動時,直線
上運動時,直線![]() 與圓
與圓![]() 恒相交,并求直線
恒相交,并求直線![]() 被圓
被圓![]() 所截得弦長
所截得弦長![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
已知直線![]() 所經過的定點
所經過的定點![]() 恰好是橢圓
恰好是橢圓![]() 的一個焦點,且橢圓
的一個焦點,且橢圓![]() 上的點到點
上的點到點![]() 的最大距離為8.
的最大距離為8.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)已知圓![]() ,直線
,直線![]() .試證明當點
.試證明當點![]() 在橢圓
在橢圓![]() 上運動時,直線
上運動時,直線![]() 與圓
與圓![]() 恒相交;并求直線
恒相交;并求直線![]() 被圓
被圓![]() 所截得的弦長的取值范圍.
所截得的弦長的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分12分)已知直線![]() 所經過的定點
所經過的定點![]() 恰好是橢圓
恰好是橢圓![]() 的一個焦點,且橢圓
的一個焦點,且橢圓![]() 上的點到點
上的點到點![]() 的最大距離為8. (1)求橢圓
的最大距離為8. (1)求橢圓![]() 的標準方程; (2)已知圓
的標準方程; (2)已知圓![]() ,直線
,直線![]() .試證明當點
.試證明當點![]() 在橢圓
在橢圓![]() 上運動時,直線
上運動時,直線![]() 與圓
與圓![]() 恒相交;并求直線
恒相交;并求直線![]() 被圓
被圓![]() 所截得的弦長的取值范圍.
所截得的弦長的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2011屆浙江省杭州市高三第二次教學質量考試數學理卷 題型:解答題
.(本題滿分14分)
已知直線
 所經過的定點
所經過的定點 恰好是橢圓
恰好是橢圓 的一個焦點,且橢圓
的一個焦點,且橢圓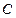 上的點到點
上的點到點 的最大距離為3.
的最大距離為3.
(Ⅰ) 求橢圓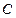 的標準方程;
的標準方程;
(Ⅱ) 設過點 的直線
的直線 交橢圓于
交橢圓于 、
、 兩點,若
兩點,若 ,求直線
,求直線 的斜率的取值范圍.
的斜率的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2010年河北省正定中學高三下學期第三次模擬考試數學(文) 題型:解答題
(本小題滿分12分)已知直線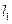
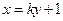 所經過的定點
所經過的定點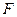 恰好是橢圓
恰好是橢圓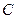 的一個焦點,且橢圓
的一個焦點,且橢圓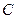 上的點到點
上的點到點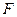 的最大距離為3.
的最大距離為3.
(Ⅰ)求橢圓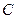 的標準方程;
的標準方程;
(Ⅱ)已知圓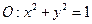 ,直線
,直線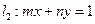 .試證明:當點
.試證明:當點 在橢圓
在橢圓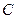 上運動時,直線
上運動時,直線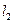 與圓
與圓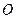 恒相交,并求直線
恒相交,并求直線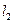 被圓
被圓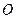 所截得弦長
所截得弦長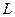 的取值范圍.
的取值范圍.
(Ⅲ)設直線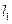 與橢圓交于
與橢圓交于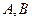 兩點,若直線
兩點,若直線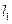 交
交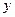 軸于點
軸于點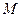 ,且
,且 ,當
,當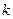 變化時,求
變化時,求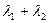 的值;
的值;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com