
 ,問題轉化為求4
,問題轉化為求4 -1值域,由此可解;
-1值域,由此可解; ,①分兩種情況討論:當
,①分兩種情況討論:當 時,當
時,當 時,;
時,; 、
、 、
、 三種情況討論求出F(x)min即可;
三種情況討論求出F(x)min即可; ,
, ,∴m<1.
,∴m<1. ,
, 即2a≥b時,F(x)max=F(1)=3a-b,
即2a≥b時,F(x)max=F(1)=3a-b, 即2a<b時,F(x)max=F(0)=b-a,
即2a<b時,F(x)max=F(0)=b-a, ;
; ,
, 即b≤0時,F(x)min+|2a-b|+a=F(0)+2a-b+a=2a>0,
即b≤0時,F(x)min+|2a-b|+a=F(0)+2a-b+a=2a>0, 即0<b<4a時,F(x)min+|2a-b|+a=F(
即0<b<4a時,F(x)min+|2a-b|+a=F(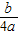 )+|2a-b|+a=
)+|2a-b|+a= ,
, 即b≥4a時,F(x)min+|2a-b|+a=F(1)+b-a=2a>0,
即b≥4a時,F(x)min+|2a-b|+a=F(1)+b-a=2a>0,

 亮點激活精編提優(yōu)100分大試卷系列答案
亮點激活精編提優(yōu)100分大試卷系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源:2012-2013學年浙江省寧波市海曙區(qū)效實中學高一(上)期中數學試卷(3-11班)(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com