設m,n∈R,若直線l:mx+ny-1=0與x軸相交于點A,與y軸相交于點B,且l與圓x2+y2=4相交所得弦的長為2,O為坐標原點,則△AOB面積的最小值為 .
【答案】
分析:由圓的方程找出圓心坐標和半徑r,由直線l被圓截得的弦長與半徑,根據垂徑定理及勾股定理求出圓心到直線l的距離,然后再利用點到直線的距離公式表示出圓心到直線l的距離,兩者相等列出關系式,整理后求出m
2+n
2的值,再由直線l與x軸交于A點,與y軸交于B點,由直線l的解析式分別令x=0及y=0,得出A的橫坐標及B的縱坐標,確定出A和B的坐標,得出OA及OB的長,根據三角形AOB為直角三角形,表示出三角形AOB的面積,利用基本不等式變形后,將m
2+n
2的值代入,即可求出三角形AOB面積的最小值.
解答:解:由圓x
2+y
2=4的方程,得到圓心坐標為(0,0),半徑r=2,
∵直線l與圓x
2+y
2=4相交所得弦CD=2,
∴圓心到直線l的距離d=
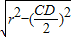
=
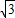
,
∴圓心到直線l:mx+ny-1=0的距離d=
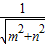
=
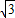
,
整理得:m
2+n
2=

,
令直線l解析式中y=0,解得:x=
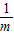
,
∴A(
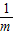
,0),即OA=
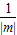
,
令x=0,解得:y=
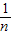
,
∴B(0,
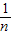
),即OB=
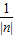
,
∵m
2+n
2≥2|mn|,當且僅當|m|=|n|時取等號,
∴|mn|≤
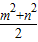
,
又△AOB為直角三角形,
∴S
△ABC=

OA•OB=
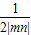
≥
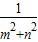
=3,
則△AOB面積的最小值為3.
故答案為:3
點評:此題考查了直線與圓相交的性質,涉及的知識有:點到直線的距離公式,垂徑定理,勾股定理,直線的一般式方程,以及基本不等式的運用,當直線與圓相交時,常常根據垂徑定理由垂直得中點,進而由弦長的一半,圓的半徑及弦心距構造直角三角形,利用勾股定理倆來解決問題.

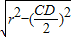 =
=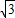 ,
,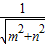 =
=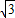 ,
, ,
,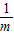 ,
,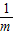 ,0),即OA=
,0),即OA=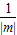 ,
,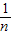 ,
,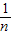 ),即OB=
),即OB=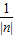 ,
,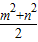 ,
, OA•OB=
OA•OB=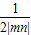 ≥
≥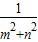 =3,
=3,

 名校課堂系列答案
名校課堂系列答案