
【題目】在直角坐標系![]() 中,橢圓
中,橢圓![]() 經過點
經過點![]() ,右焦點
,右焦點![]() 到右準線和左頂點的距離相等,經過點
到右準線和左頂點的距離相等,經過點![]() 的直線
的直線![]() 交橢圓于點
交橢圓于點![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)點![]() 是直線
是直線![]() 上在橢圓外的一點,且
上在橢圓外的一點,且![]() ,證明:點
,證明:點![]() 在定直線上.
在定直線上.
【答案】(1)![]() (2)詳見解析
(2)詳見解析
【解析】
(1)根據點在橢圓上以及右焦點![]() 到右準線和左頂點的距離相等列方程組可解得;
到右準線和左頂點的距離相等列方程組可解得;
(2)當直線![]() 軸時,將
軸時,將![]() 用
用![]() 表示后,代入
表示后,代入![]() 不成立, 當直線
不成立, 當直線![]() 與
與![]() 軸不垂直時,設出直線
軸不垂直時,設出直線![]() 的方程
的方程![]() ,與橢圓方程聯立,利用韋達定理以及
,與橢圓方程聯立,利用韋達定理以及![]() ,
,![]() ,
,![]() ,代入
,代入![]() 可解得.
可解得.
(1)依題意可列方程組: ,所以
,所以 ,
,
所以 ,所以
,所以 ,又
,又![]() ,所以
,所以![]() ,解得
,解得![]() ,
,
所以橢圓![]() 的標準方程為:
的標準方程為:![]() .
.
(2)證明:設![]() ,
,
當直線![]() 軸,則
軸,則![]() ,
,![]() ,則
,則![]() ,
,
因為![]() 在橢圓外,所以
在橢圓外,所以![]() 與
與![]() 同號,所以
同號,所以![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() 不成立,故直線
不成立,故直線![]() 與
與![]() 軸不垂直.
軸不垂直.
當直線![]() 與
與![]() 軸不垂直時,設
軸不垂直時,設![]() ,
,
設直線![]() 的方程為
的方程為![]() ,與橢圓
,與橢圓![]() 聯立消去
聯立消去![]() 并整理得,
并整理得,
![]() ,
,
因為![]() ,
,
所以![]() ,
,
所以![]() ,
,
同理可得:![]() ,
,![]() .
.
因為點![]() 在橢圓外,所以
在橢圓外,所以![]() 、
、![]() 同號,
同號,
所以![]()
 ,
,
由![]() 得,
得,
 ,
,
所以![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以![]() ,所以點
,所以點![]() 在定直線
在定直線![]() 上.
上.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】某校高一年級有甲,乙,丙三位學生,他們前三次月考的物理成績如表:
第一次月考物理成績 | 第二次月考物理成績 | 第三次月考物理成績 | |
學生甲 | 80 | 85 | 90 |
學生乙 | 81 | 83 | 85 |
學生丙 | 90 | 86 | 82 |
則下列結論正確的是( )
A. 甲,乙,丙第三次月考物理成績的平均數為86
B. 在這三次月考物理成績中,甲的成績平均分最高
C. 在這三次月考物理成績中,乙的成績最穩定
D. 在這三次月考物理成績中,丙的成績方差最大
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的右焦點為
的右焦點為![]() ,過點
,過點![]() 且與
且與![]() 軸垂直的直線被橢圓截得的線段長為
軸垂直的直線被橢圓截得的線段長為![]() ,且
,且![]() 與短軸兩端點的連線相互垂直.
與短軸兩端點的連線相互垂直.
(1)求橢圓![]() 的方程;
的方程;
(2)若圓![]() 上存在兩點
上存在兩點![]() ,
,![]() ,橢圓
,橢圓![]() 上存在兩個點
上存在兩個點![]() 滿足:
滿足:![]() 三點共線,
三點共線,![]() 三點共線,且
三點共線,且![]() ,求四邊形
,求四邊形![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《周髀算經》 是我國古代的天文學和數學著作。其中一個問題的大意為:一年有二十四個節氣(如圖),每個節氣晷長損益相同(即物體在太陽的照射下影子長度的增加量和減少量相同).若冬至晷長一丈三尺五寸,夏至晷長一尺五寸(注:ー丈等于十尺,一尺等于十寸),則立冬節氣的晷長為( )
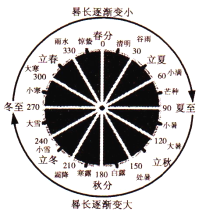
A. 九尺五寸 B. 一丈五寸 C. 一丈一尺五寸 D. 一丈六尺五寸
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為迎接“五一”節的到來,某單位舉行“慶五一,展風采”的活動.現有6人參加其中的一個節目,該節目由![]() 兩個環節可供參加者選擇,為增加趣味性,該單位用電腦制作了一個選擇方案:按下電腦鍵盤“Enter”鍵則會出現模擬拋兩枚質地均勻骰子的畫面,若干秒后在屏幕上出現兩個點數
兩個環節可供參加者選擇,為增加趣味性,該單位用電腦制作了一個選擇方案:按下電腦鍵盤“Enter”鍵則會出現模擬拋兩枚質地均勻骰子的畫面,若干秒后在屏幕上出現兩個點數![]() 和
和![]() ,并在屏幕的下方計算出
,并在屏幕的下方計算出![]() 的值.現規定:每個人去按“Enter”鍵,當顯示出來的
的值.現規定:每個人去按“Enter”鍵,當顯示出來的![]() 小于
小于![]() 時則參加
時則參加![]() 環節,否則參加
環節,否則參加![]() 環節.
環節.
(1)求這6人中恰有2人參加該節目![]() 環節的概率;
環節的概率;
(2)用![]() 分別表示這6個人中去參加該節目
分別表示這6個人中去參加該節目![]() 兩個環節的人數,記
兩個環節的人數,記![]() ,求隨機變量
,求隨機變量![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】出版商為了解某科普書一個季度的銷售量![]() (單位:千本)和利潤
(單位:千本)和利潤![]() (單位:元/本)之間的關系,對近年來幾次調價之后的季銷售量進行統計分析,得到如下的10組數據.
(單位:元/本)之間的關系,對近年來幾次調價之后的季銷售量進行統計分析,得到如下的10組數據.
序號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2.4 | 3.1 | 4.6 | 5.3 | 6.4 | 7.1 | 7.8 | 8.8 | 9.5 | 10 |
| 18.1 | 14.1 | 9.1 | 7.1 | 4.8 | 3.8 | 3.2 | 2.3 | 2.1 | 1.4 |
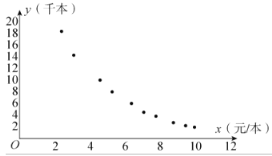
根據上述數據畫出如圖所示的散點圖:
(1)根據圖中所示的散點圖判斷![]() 和
和![]() 哪個更適宜作為銷售量
哪個更適宜作為銷售量![]() 關于利潤
關于利潤![]() 的回歸方程類型?(給出判斷即可,不需要說明理由)
的回歸方程類型?(給出判斷即可,不需要說明理由)
(2)根據(1)中的判斷結果及參考數據,求出![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(3)根據回歸方程設該科普書一個季度的利潤總額為![]() (單位:千元),當季銷售量
(單位:千元),當季銷售量![]() 為何值時,該書一個季度的利潤總額預報值最大?(季利潤總額=季銷售量×每本書的利潤)
為何值時,該書一個季度的利潤總額預報值最大?(季利潤總額=季銷售量×每本書的利潤)
參考公式及參考數據:
①對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的公式分別為
的斜率和截距的公式分別為 .
.
②參考數據:
|
|
|
|
|
|
|
6.50 | 6.60 | 1.75 | 82.50 | 2.70 |
|
|
表中![]() .另:
.另:![]() .計算時,所有的小數都精確到0.01.
.計算時,所有的小數都精確到0.01.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對某兩名高三學生連續9次數學測試的成績(單位:分)進行統計得到如下折線圖.下列有關這兩名學生數學成績的分析中,正確的結論是( )
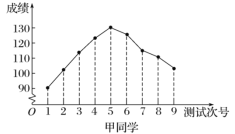
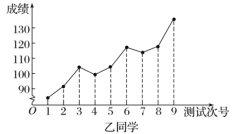
A.甲同學的成績折線圖具有較好的對稱性,與正態曲線相近,故而平均成績為130分
B.根據甲同學成績折線圖中的數據進行統計,估計該同學平均成績在區間![]() 內
內
C.乙同學的數學成績與測試次號具有比較明顯的線性相關性,且為正相關
D.乙同學在這連續九次測驗中的最高分與最低分的差超過40分
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com