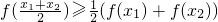B
分析:對于①A,B是該圖象上的任意兩點,直線AB的斜率可以用AB中點對應的橫坐標對應到圖象上點的切線斜率近似代替,根據函數的導數是一個減函數,知當x<0時f′(x)>f′(0)=1,故①不正確;再結合選項,說明應在B、C當中選一個,問題的焦點集中到③這個命題是否正確了.利用函數圖象的凹凸性不難發現命題③是正確的,這樣就可以選到正確答案了.
解答:先看命題①:若A,B是該圖象上的任意兩點,直線AB的斜率可以用AB中點對應的橫坐標對應到圖象上點的切線斜率近似代替,
由已知條件曲線在原點處的切線的方程為y=x,說明f′(0)=1,再根據函數的導數是一個減函數知
當x<0時f′(x)>f′(0)=1,說明存在-5<x<0時直線AB的斜率k
AB>1,故①不正確;
再結合選項:只有B、C當中沒有認為①正確,說明應在B、C當中選一個,
問題的焦點集中到③這個命題是否正確了.
利用函數圖象的凹凸性:函數f(x)是一個凸函數,說明滿足不等式:
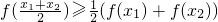
對照一下命題③,說明命題③是正確的,因此可得正確答案為②③④.
故選B
點評:本題考查了利用導數研究函數的圖象、函數圖象的凹凸性和函數恒成立等問題,綜合性較強,是一道難題.此問題還著重考查學生觀察圖形,分析問題和解決問題的能力,不失為一道優良的考題.

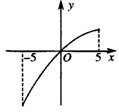 函數y=f(x),x∈[-5,5]的圖象如圖所示,該曲線在原點處的切線的方程為y=x,且導函數f′(x)是減函數.給出下列四個命題:
函數y=f(x),x∈[-5,5]的圖象如圖所示,該曲線在原點處的切線的方程為y=x,且導函數f′(x)是減函數.給出下列四個命題: )恒成立;
)恒成立;