
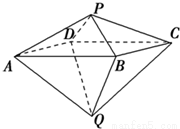
 如圖,已知兩個正四棱錐P-ABCD與Q-ABCD的高分別為1和2,AB=4.
如圖,已知兩個正四棱錐P-ABCD與Q-ABCD的高分別為1和2,AB=4.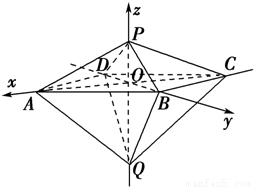 法一:(Ⅰ)連接AC、BD,設AC∩BD=O.證明PQ⊥平面ABCD,只需說明P、O、Q三點在一條直線上,QO⊥平面ABCD即可;
法一:(Ⅰ)連接AC、BD,設AC∩BD=O.證明PQ⊥平面ABCD,只需說明P、O、Q三點在一條直線上,QO⊥平面ABCD即可;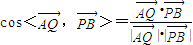 ,求異面直線AQ與PB所成的角;
,求異面直線AQ與PB所成的角;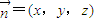 是平面QAD的一個法向量,利用
是平面QAD的一個法向量,利用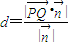 ,求點P到平面QAD的距離.
,求點P到平面QAD的距離.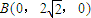
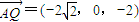 ,
,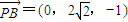 ,
,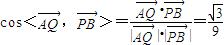 .
.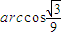 .
.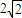 ,0),
,0),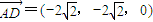 ,
,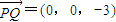 ,
,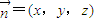 是平面QAD的一個法向量,
是平面QAD的一個法向量,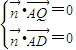 得
得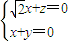 .
.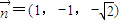 .
.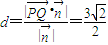 ..
..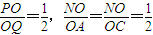 ,
,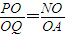 ,
,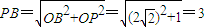 .
.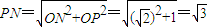
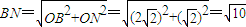
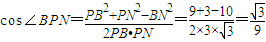 .
.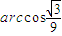 .
.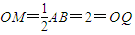 .
.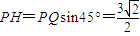 .
.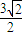


 期末寶典單元檢測分類復習卷系列答案
期末寶典單元檢測分類復習卷系列答案科目:高中數學 來源: 題型:
 我們將底面是正方形,側棱長都相等的棱錐稱為正四棱錐.已知由兩個完全相同的正四棱錐組合而成的空間幾何體的正視圖、側視圖、俯視圖都相同,且如圖所示,視圖中四邊形ABCD是邊長為1的正方形,則該幾何體的體積為( )
我們將底面是正方形,側棱長都相等的棱錐稱為正四棱錐.已知由兩個完全相同的正四棱錐組合而成的空間幾何體的正視圖、側視圖、俯視圖都相同,且如圖所示,視圖中四邊形ABCD是邊長為1的正方形,則該幾何體的體積為( )查看答案和解析>>
科目:高中數學 來源: 題型:
 (2008•奉賢區二模)如圖,在正四棱柱ABCD-A1B1C1D1中,AB=4,AA1=8.
(2008•奉賢區二模)如圖,在正四棱柱ABCD-A1B1C1D1中,AB=4,AA1=8.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
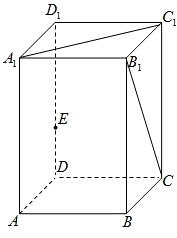 如圖,在正四棱柱ABCD-A1B1C1D1中,AB=4,AA1=8.
如圖,在正四棱柱ABCD-A1B1C1D1中,AB=4,AA1=8.查看答案和解析>>
科目:高中數學 來源:2012-2013學年福建省福州三中高三(上)期中數學試卷(解析版) 題型:選擇題





查看答案和解析>>
科目:高中數學 來源:2008年上海市奉賢區高考數學二模試卷(文科)(解析版) 題型:解答題
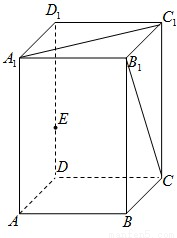
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com