（本題滿分13分，第（1）小題5分，第（2）小題8分）
設復數
(1)當
時，求
的值；
(2)若復數
所對應的點在直線
上，求
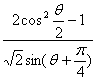的值。
科目：高中數學 來源： 題型：
(本題滿分13分)本題共有2個小題，第一個小題滿分5分，第2個小題滿分8分。
已知數列
的前
項和為
，且
，
（1）證明：
是等比數列；
（2）求數列
的通項公式，并求出n為何值時，取得最小值，并說明理由。
（2）=
n=15取得最小值
查看答案和解析>>
科目：高中數學 來源：2011年福建省高二上學期期末考試數學理卷 題型：解答題
（本題滿分13分）在4月份（按30天計算），有一新款服裝投入某商場銷售，4月1日該款服裝僅銷售出10件，第二天售出35件，第三天銷售60件，然后，每天售出的件數分別遞增25件，直到4月12日銷售量達到最大，以后每天銷售的件數分別遞減15件.
（Ⅰ）問到月底該服裝共銷售出幾件．
（Ⅱ）按規(guī)律，當該商場銷售此服裝的日銷售量達到150件以上時，社會上就流行，問該款服裝在社會上流行是否超過14天？并說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
（本題滿分13分，第（1）小題6分，第（2）小題7分）
為了降低能源損耗，最近上海對新建住宅的屋頂和外墻都要求建造隔熱層．某幢建筑物要建造可使用20年的隔熱層，每厘米厚的隔熱層建造成本為6萬元．該建筑物每年的能源消耗費用C（單位：萬元）與隔熱層厚度
（單位：cm）滿足關系：
，若不建隔熱層，每年能源消耗費用為8萬元．設
為隔熱層建造費用與20年的能源消耗費用之和．
（1）求
的值及的表達式；
（2）隔熱層修建多厚時，總費用達到最小，并求最小值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
，
。
。
。
展開式中，求：