
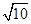 .
.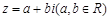 對應的點為
對應的點為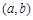 ,所以有
,所以有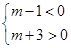 ,從而可解得m的取值范圍為(-3,1),(2)因為命題“p且q”一假就假,所以p,q中至少有一個為假;因為命題“p或q”一真就真,所以p,q中至少有一個為真;綜合得p,q中一真一假.若q為真,則q為假;或若q為假,則q為真.先求命題為真時參數范圍,再根據集合的補集求命題為假時參數范圍.
,從而可解得m的取值范圍為(-3,1),(2)因為命題“p且q”一假就假,所以p,q中至少有一個為假;因為命題“p或q”一真就真,所以p,q中至少有一個為真;綜合得p,q中一真一假.若q為真,則q為假;或若q為假,則q為真.先求命題為真時參數范圍,再根據集合的補集求命題為假時參數范圍.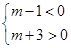
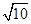 ,
,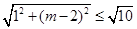 ,解得-1≤m≤5. 5分
,解得-1≤m≤5. 5分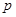 真
真 假或
假或 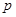 假
假 真,所以
真,所以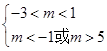 或
或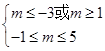


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com