
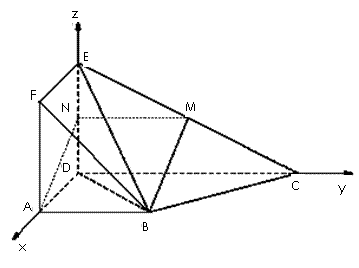
(12分)如圖正方形ADEF與梯形ABCD所在的平面互相垂直,AD⊥CD, AB//CD,AB=AD=2,CD=4,M為CE的中點。
(I)求證:BM//平面ADEF;
(II)求證:平面![]() 平面BEC;
平面BEC;
(III)求平面BEC與平面ADEF所成銳二面角的余弦值。

(1)證明:取DE中點N,連結(jié)MN,AN
 |
在ΔEDC中,M、N分別為EC, ED的中點,所以MN//CD,且MN=![]() CD.
CD.
由已知AB//CD, AB=![]() CD,所以MN//AB, 且MN=AB。
CD,所以MN//AB, 且MN=AB。
所以四邊形ABMN為平行四邊形,所以BM//AN
又因為AN![]() 平面ADEF,
平面ADEF,
且BM![]() 平面ADEF,
平面ADEF,
所以BM//平面ADEF。……(4分)
(2)證明:
在正方形ADEF中,ED⊥AD,
又因為平面ADEF⊥平面ABCD,
且平面ADEF∩平面ABCD=AD,
所以ED⊥平面ABCD,所以ED⊥BC.
在直角梯形ABCD中,
AB=AD=2, CD=4,可得BC=![]()
在ΔBCD中,BD=BC=![]() ,CD=4,
,CD=4,
所以BC⊥BD。
所以BC⊥平面BDE,又因為BC![]() 平面BCE,
平面BCE,
所以平面BDE⊥平面BEC。 ……(9分)
(3)由(2)知ED⊥平面ABCD,且AD⊥CD。
以D為原點,DA, DC, DE所在直線為x,y,z軸,建立空間直角坐標系。
B(2,2,0), C(0,4,0), E(0,0,2),平面ADEF的一個法向量為m=(0,1,0).
設n=(x,y,z)為平面BEC的一個法向量,因為![]()
![]()
所以n=(1,1,2)為平面BEC的一個法向量
設平面BEC與平面ADEF所成銳二面角為![]()
則![]()
所以平面BEC與平面ADEF所成銳二面角為余弦值為![]()


 雙基同步導航訓練系列答案
雙基同步導航訓練系列答案 黃岡小狀元同步計算天天練系列答案
黃岡小狀元同步計算天天練系列答案科目:高中數(shù)學 來源: 題型:
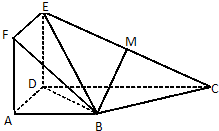 如圖正方形ADEF與梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,
如圖正方形ADEF與梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源:2013-2014學年云南省部分名校高三12月聯(lián)考理科數(shù)學試卷(解析版) 題型:解答題
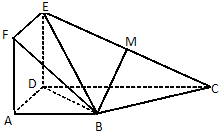
如圖,正方形ADEF與梯形ABCD所在的平面互相垂直,AD丄CD,AB//CD,AB=AD=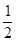 CD=2,點M在線段EC上.
CD=2,點M在線段EC上.
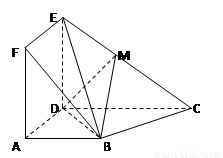
(I)當點M為EC中點時,求證: 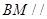 面
面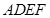 ;
;
(II)求證:平面BDE丄平面BEC;
(III)若平面說BDM與平面ABF所成二面角銳角,且該二面角的余弦值為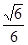 時,求三棱錐M-BDE的體積.
時,求三棱錐M-BDE的體積.
查看答案和解析>>
科目:高中數(shù)學 來源:2010-2011學年北京市東城區(qū)高三(上)期末數(shù)學試卷(理科)(解析版) 題型:解答題
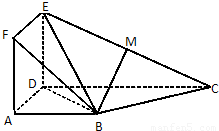 如圖正方形ADEF與梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,
如圖正方形ADEF與梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,查看答案和解析>>
科目:高中數(shù)學 來源:2010-2011學年江西省宜春市上高二中高三(下)第六次月考數(shù)學試卷(理科)(解析版) 題型:解答題
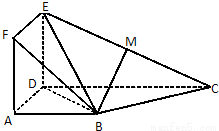 如圖正方形ADEF與梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,
如圖正方形ADEF與梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com