Question

已知ABCD-A₁B₁C₁D₁ 是底面邊長為1的正四棱柱，高AA₁=2，求
（1）異面直線BD 與AB₁ 所成角的大小（結果用反三角函數值表示）；
（2）四面體AB₁D₁C 的體積．

Answer 1

分析：（1）根據題意知DC₁∥AB₁∴∠BDC₁就是異面直線BD 與AB₁ 所成角，解三角形即可求得結果．
（2）V_A-B1D1C=V_{ABCD-A1B1C1D1}-V_B1-ABC-V_D1-ACD-V_DA1C1D1-V_B-A1B1C1，
而V_{ABCD-A1B1C1D1}-V_B1-ABC-V_D1-ACD-V_DA1C1D1-V_B-A1B1C1易求，即可求得四面體AB₁D₁C 的體積．

解答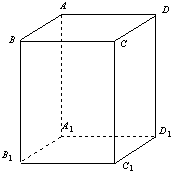：解：（1）連接DC₁，BC₁，
易知DC₁∥AB₁，
∴∠BDC₁就是異面直線BD 與AB₁ 所成角，
在△BDC₁中，DC₁=BC₁=

5

，BD=

2

，
∴cos∠BDC₁=

2 2

5

=

10

10

，
∴∠BDC₁=arccos

10

10

．

（2）V_A-B1D1C=V_{ABCD-A1B1C1D1}-V_B1-ABC-V_D1-ACD-V_DA1C1D1-V_B-A1B1C1
而V_{ABCD-A1B1C1D1}=S_ABCD•AA₁=1×2=2，
V_B1-ABC=V_D1-ACD=V_DA1C1D1=V_B-A1B1C1=

1

3

×

1

2

×2
∴V_A-B1D1C=2-4×

1

3

×

1

2

×2=

2

3

．

點評：此題是個基礎題．考查異面直線所成角和棱錐的體積問題，求解方法一般是平移法，轉化為平面角問題來解決，和利用割補法求棱錐的體積問題，體現了數形結合和轉化的思想．