
 、
、 、
、 ;已知乙項目的利潤與產品價格的調整有關,在每次調整中價格下降的概率都是P(0<P<1),設乙項目產品價格在一年內進行2次獨立的調整,記乙項目產品價格在一年內的下降次數為ζ,對乙項目每投資十萬元,ξ取0、1、2時,一年后相應利潤是1.3萬元、1.25萬元、0.2萬元.隨機變量ξ1、ξ2分別表示對甲、乙兩項目各投資十萬元一年后的利潤.
;已知乙項目的利潤與產品價格的調整有關,在每次調整中價格下降的概率都是P(0<P<1),設乙項目產品價格在一年內進行2次獨立的調整,記乙項目產品價格在一年內的下降次數為ζ,對乙項目每投資十萬元,ξ取0、1、2時,一年后相應利潤是1.3萬元、1.25萬元、0.2萬元.隨機變量ξ1、ξ2分別表示對甲、乙兩項目各投資十萬元一年后的利潤.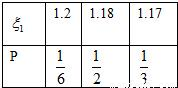
 +1.18×
+1.18× +1.17×
+1.17× =1.18.
=1.18.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
(08年長沙市模擬理)(12分)現有甲、乙兩個項目,對甲項目每投資十萬元,一年后利潤是1.2萬元,1.18萬元,1.17萬元的概率分別為![]() ;已知乙項目的利潤與產品價格調整有關,在每次調整中價格下降的概率為P(0<P<1),記乙項目產品價格在一年內進行2次獨立調整,設乙項目產品價格在一年內的下降次數為
;已知乙項目的利潤與產品價格調整有關,在每次調整中價格下降的概率為P(0<P<1),記乙項目產品價格在一年內進行2次獨立調整,設乙項目產品價格在一年內的下降次數為![]() ,對乙項目再投資十萬元,
,對乙項目再投資十萬元,![]() 以0,1,2時產品價格在一年后的利潤是1.3萬元,1.25萬元,0.2萬元。隨機變量
以0,1,2時產品價格在一年后的利潤是1.3萬元,1.25萬元,0.2萬元。隨機變量![]() 1,
1,![]() 2分別表示甲、乙兩項目各投資十萬元一年后的利潤。
2分別表示甲、乙兩項目各投資十萬元一年后的利潤。
(1)求![]() 1,
1,![]() 2的概率分布列和數學期望E
2的概率分布列和數學期望E![]() 1,E
1,E![]() 2;
2;
(2)當E![]() 1,E
1,E![]() 2時,求P的范圍。
2時,求P的范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
現有甲、乙兩個項目,對甲項目每投資十萬元,一年后利潤是1.2萬元、1.18萬元、1.17萬元的概率分別為![]() 、
、![]() 、
、![]() ;已知乙項目的利潤與產品價格的調整有關,在每次調整中價格下降的概率都是
;已知乙項目的利潤與產品價格的調整有關,在每次調整中價格下降的概率都是![]() ,設乙項目產品價格在一年內進行2次獨立的調整,記乙項目產品價格在一年內的下降次數為
,設乙項目產品價格在一年內進行2次獨立的調整,記乙項目產品價格在一年內的下降次數為![]() ,對乙項目每投資十萬元,
,對乙項目每投資十萬元, ![]() 取0、1、2時, 一年后相應利潤是1.3萬元、1.25萬元、0.2萬元.隨機變量
取0、1、2時, 一年后相應利潤是1.3萬元、1.25萬元、0.2萬元.隨機變量![]() 、
、![]() 分別表示對甲、乙兩項目各投資十萬元一年后的利潤.
分別表示對甲、乙兩項目各投資十萬元一年后的利潤.
(I) 求![]() 、
、![]() 的概率分布和數學期望
的概率分布和數學期望![]() 、
、![]() ;
;
(II) 當![]()
![]()
![]() 時,求
時,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
現有甲、乙兩個項目,對甲項目每投資十萬元,一年后利潤是1.2萬元、1.18萬元、1.17萬元的概率分別為![]() 、
、![]() 、
、![]() ;已知乙項目的利潤與產品價格的調整有關,在每次調整中價格下降的概率都是
;已知乙項目的利潤與產品價格的調整有關,在每次調整中價格下降的概率都是![]() ,設乙項目產品價格在一年內進行2次獨立的調整,記乙項目產品價格在一年內的下降次數為
,設乙項目產品價格在一年內進行2次獨立的調整,記乙項目產品價格在一年內的下降次數為![]() ,對乙項目每投資十萬元,
,對乙項目每投資十萬元, ![]() 取0、1、2時, 一年后相應利潤是1.3萬元、1.25萬元、0.2萬元.隨機變量
取0、1、2時, 一年后相應利潤是1.3萬元、1.25萬元、0.2萬元.隨機變量![]() 、
、![]() 分別表示對甲、乙兩項目各投資十萬元一年后的利潤.
分別表示對甲、乙兩項目各投資十萬元一年后的利潤.
(I) 求![]() 、
、![]() 的概率分布和數學期望
的概率分布和數學期望![]() 、
、![]() ;
;
(II) 當![]() 時,求
時,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2013屆福建省高二下學期期末理科數學試卷(解析版) 題型:解答題
(本小題滿分13分)
現有甲、乙兩個項目,對甲項目投資十萬元,一年后利潤是1.2萬元、1.18萬元、1.17萬元的概率分別為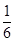 、
、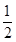 、
、 ;已知乙項目的利潤與產品價格的調整有關,在每次調整中價格下降的概率都是
;已知乙項目的利潤與產品價格的調整有關,在每次調整中價格下降的概率都是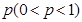 ,設乙項目產品價格在一年內進行2次獨立的調整,記乙項目產品價格在一年內的下降次數為
,設乙項目產品價格在一年內進行2次獨立的調整,記乙項目產品價格在一年內的下降次數為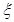 ,對乙項目投資十萬元,
,對乙項目投資十萬元, 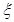 取0、1、2時, 一年后相應利潤是1.3萬元、1.25萬元、0.2萬元.隨機變量
取0、1、2時, 一年后相應利潤是1.3萬元、1.25萬元、0.2萬元.隨機變量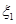 、
、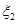 分別表示對甲、乙兩項目各投資十萬元一年后的利潤.
分別表示對甲、乙兩項目各投資十萬元一年后的利潤.
(I) 求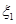 、
、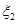 的概率分布和數學期望
的概率分布和數學期望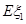 、
、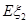 ;
;
(II)當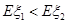 時,求
時,求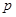 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com