【答案】
分析:(1)先確定函數的定義域然后求導數fˊ(x),令g(x)=2x
2+2x+a,由題意知x
1、x
2是方程g(x)=0的兩個均大于-1的不相等的實根,建立不等關系解之即可,在函數的定義域內解不等式fˊ(x)>0和fˊ(x)<0,求出單調區間;
(2)x
2是方程g(x)=0的根,將a用x
2表示,消去a得到關于x
2的函數,研究函數的單調性求出函數的最大值,即可證得不等式.
解答:解:(I)
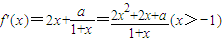
令g(x)=2x
2+2x+a,其對稱軸為
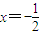
.
由題意知x
1、x
2是方程g(x)=0的兩個均大于-1的不相等的實根,
其充要條件為
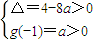
,得
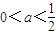
(1)當x∈(-1,x
1)時,f'(x)>0,∴f(x)在(-1,x
1)內為增函數;
(2)當x∈(x
1,x
2)時,f'(x)<0,∴f(x)在(x
1,x
2)內為減函數;
(3)當x∈(x
2,+∞)時,f'(x)>0,∴f(x)在(x
2,+∞)內為增函數;
(II)由(I)
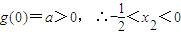
,a=-(2x
22+2x
2)
∴f(x
2)=x
22+aln(1+x
2)=x
22-(2x
22+2x
2)ln(1+x
2)
設
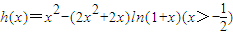
,
則h'(x)=2x-2(2x+1)ln(1+x)-2x=-2(2x+1)ln(1+x)
(1)當
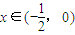
時,h'(x)>0,∴h(x)在
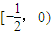
單調遞增;
(2)當x∈(0,+∞)時,h'(x)<0,h(x)在(0,+∞)單調遞減.∴
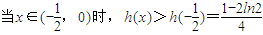
故
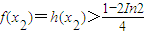
.
點評:本題主要考查了利用導數研究函數的單調性,以及利用導數研究函數的極值等有關知識,屬于基礎題.

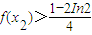 .
.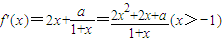
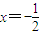 .
.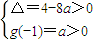 ,得
,得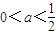
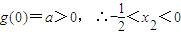 ,a=-(2x22+2x2)
,a=-(2x22+2x2)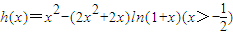 ,
,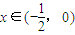 時,h'(x)>0,∴h(x)在
時,h'(x)>0,∴h(x)在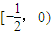 單調遞增;
單調遞增;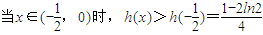
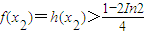 .
.

 云南師大附小一線名師提優作業系列答案
云南師大附小一線名師提優作業系列答案 沖刺100分單元優化練考卷系列答案
沖刺100分單元優化練考卷系列答案