
已知函數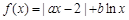 (x>0).
(x>0).
(1)若a=1,f(x)在(0,+∞)上是單調增函數,求b的取值范圍;
(2)若a≥2,b=1,求方程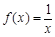 在(0,1]上解的個數.
在(0,1]上解的個數.
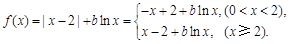
1/當0<x<2時,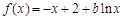 ,
,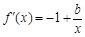 .由條件,得
.由條件,得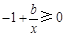 恒成立,
恒成立,
即b≥x恒成立.∴b≥2. …………… 2分
② 當x≥2時, ,
,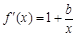 .由條件,得
.由條件,得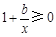 恒成立,
恒成立,
即b≥-x恒成立.∴b≥-2.…………… 4分
綜合①,②得b的取值范圍是b≥2. …………………… 5分
(2)令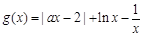 ,即
,即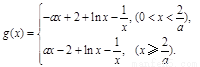
當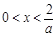 時,
時,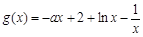 ,.
,.
∵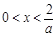 ,∴
,∴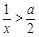 .則
.則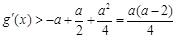 ≥0.
≥0.
即 ,∴
,∴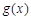 在(0,
在(0, )上是遞增函數. ………………… 7分
)上是遞增函數. ………………… 7分
當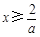 時,
時,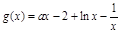 ,
,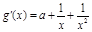 >0.∴
>0.∴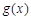 在(
在( ,+∞)上是遞增函數.又因為函數g(x)在
,+∞)上是遞增函數.又因為函數g(x)在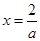 有意義,∴
有意義,∴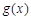 在(0,+∞)上是遞增函數.…… 10分
在(0,+∞)上是遞增函數.…… 10分
∵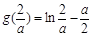 ,而a≥2,∴
,而a≥2,∴ ,則
,則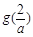 <0.∵a≥2,∴
<0.∵a≥2,∴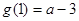 ……
12分
……
12分
當a≥3時,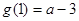 ≥0,∴g(x)=0在
≥0,∴g(x)=0在 上有惟一解.當
上有惟一解.當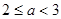 時,
時,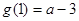 <0,∴g(x)=0在
<0,∴g(x)=0在 上無解
上無解
【解析】略


 導學與測試系列答案
導學與測試系列答案 新非凡教輔沖刺100分系列答案
新非凡教輔沖刺100分系列答案科目:高中數學 來源: 題型:
|
查看答案和解析>>
科目:高中數學 來源: 題型:
| π |
| 2 |
| π |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| x |
查看答案和解析>>
科目:高中數學 來源: 題型:
(08年周至二中三模理) 已知函數f (x)(0≤x≤1)的圖象的一段圓弧(如圖所示)若![]() ,則 ( )
,則 ( )
(A)![]() (B)
(B)![]()
(C)![]() (D)前三個判斷都不正確
(D)前三個判斷都不正確

查看答案和解析>>
科目:高中數學 來源: 題型:
(14分)已知函數![]() ,( x>0).
,( x>0).
(I)當0<a<b,且f(a)=f(b)時,求證:ab>1;
(II)是否存在實數a,b(a<b),使得函數y=f(x)的定義域、值域都是[a,b],若存在,則求出a,b的值,若不存在,請說明理由.
(III)若存在實數a,b(a<b),使得函數y=f(x)的定義域為 [a,b]時,值域為 [ma,mb]
(m≠0),求m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com