
【題目】已知常數![]() ,數列
,數列![]() 滿足
滿足![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 的值;
的值;
(2)在(1)的條件下,求數列![]() 的前
的前![]() 項和
項和![]() ;
;
(3)若數列![]() 中存在三項
中存在三項![]() ,
,![]() ,
,![]() (
(![]() 且
且![]() )依次成等差數列,求
)依次成等差數列,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() .
.
【解析】
(1)根據題中條件,逐項計算,即可得出結果;
(2)由(1)得到![]() ,
,![]() ,當
,當![]() 時,
時,![]() ,從而
,從而![]() ,得出
,得出![]() ,由等比數列的求和公式,即可得出結果;
,由等比數列的求和公式,即可得出結果;
(3)先由![]() ,得到數列
,得到數列![]() 是遞增數列,分
是遞增數列,分![]() ,
,![]() ,
,![]() 三種情況,利用放縮法,以及等差中項的概念,即可得出結果.
三種情況,利用放縮法,以及等差中項的概念,即可得出結果.
(1)因為![]() ,
,![]() ,
,
所以![]() ,
,
因此![]() ,
,![]() ,
,
![]() ;
;
(2)因為![]() ,
,![]() ,
,
所以,當![]() 時,
時,![]() ,從而
,從而![]() ,
,
于是有:![]() ;
;
當![]() 時,
時,![]() ;
;
當![]() 時,
時,![]() ,
,
所以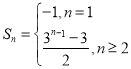 ,即
,即![]() ,
,![]() ;
;
(3)因為![]() ,
,
所以![]() ,即數列
,即數列![]() 是遞增數列,
是遞增數列,
①當![]() 時,有
時,有![]() ,于是有
,于是有![]() ,
,
從而![]() ,
,
所以![]() ,
,
若數列![]() 中存在三項
中存在三項![]() ,
,![]() ,
,![]() (
(![]() 且
且![]() )依次成等差數列,
)依次成等差數列,
則有![]() ,即
,即![]() ,
,
因為![]() ,所以
,所以![]() ,
,
所以![]() 不成立,因此此時數列
不成立,因此此時數列![]() 中不存在三項
中不存在三項![]() ,
,![]() ,
,![]() (
(![]() 且
且![]() )依次成等差數列;
)依次成等差數列;
②當![]() 時,有
時,有![]() ,
,
此時![]() ,
,
于是當![]() 時,
時,![]() ,從而
,從而![]() ,
,
所以![]() ,
,
若數列![]() 中存在三項
中存在三項![]() ,
,![]() ,
,![]() (
(![]() 且
且![]() )依次成等差數列,
)依次成等差數列,
則有![]() ,同①可知:
,同①可知:![]() ,于是有
,于是有![]() ,
,
因為![]() ,所以
,所以![]() ,
,
因為![]() 是整數,所以
是整數,所以![]() ,
,
于是![]() ,即
,即![]() 與
與![]() 矛盾,
矛盾,
故此時數列![]() 中不存在三項
中不存在三項![]() ,
,![]() ,
,![]() (
(![]() 且
且![]() )依次成等差數列;
)依次成等差數列;
③當![]() 時,有
時,有![]() ,
,![]() ,
,
于是![]() ,
,
![]() ,
,
此時數列![]() 中存在三項
中存在三項![]() ,
,![]() ,
,![]() (
(![]() 且
且![]() )依次成等差數列,
)依次成等差數列,
綜上,![]() .
.


 名師點撥卷系列答案
名師點撥卷系列答案科目:高中數學 來源: 題型:
【題目】平面直角坐標系中,直線![]() 的參數方程為
的參數方程為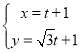 ,(
,(![]() 為參數).以原點為極點,
為參數).以原點為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出直線![]() 的極坐標方程與曲線
的極坐標方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)已知與直線![]() 平行的直線
平行的直線![]() 過點
過點![]() ,且與曲線
,且與曲線![]() 交于
交于![]() 兩點,試求
兩點,試求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若有窮數列![]() (
(![]() )滿足:①
)滿足:①![]() ;②
;②![]() .則稱該數列為“
.則稱該數列為“![]() 階非凡數列”
階非凡數列”
(1)分別寫出一個單調遞增的“![]() 階非凡數列”和一個單調遞減的“
階非凡數列”和一個單調遞減的“![]() 階非凡數列”;
階非凡數列”;
(2)設![]() ,若“
,若“![]() 階非凡數列”是等差數列,求其通項公式;
階非凡數列”是等差數列,求其通項公式;
(3)記“![]() 階非凡數列”的前
階非凡數列”的前![]() 項的和為
項的和為![]() ,求證:
,求證:![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位有員工1000名,平均每人每年創造利潤10萬元,為了增加企業競爭力,決定優化產業結構,調整出![]() (
(![]() )名員工從事第三產業,調整后這
)名員工從事第三產業,調整后這![]() 名員工他們平均每人創造利潤為
名員工他們平均每人創造利潤為![]() 萬元,剩下的員工平均每人每年創造的利潤可以提高
萬元,剩下的員工平均每人每年創造的利潤可以提高![]() .
.
(1)若要保證剩余員工創造的年總利潤不低于原來1000名員工創造的年總利潤,則最多調整多少名員工從事第三產業?
(2)設![]() ,若調整出的員工創造出的年總利潤始終不高于剩余員工創造的年總利潤,求
,若調整出的員工創造出的年總利潤始終不高于剩余員工創造的年總利潤,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某海域有![]() 兩個島嶼,
兩個島嶼,![]() 島在
島在![]() 島正東4海里處,經多年觀察研究發現,某種魚群洄游的路線是曲線
島正東4海里處,經多年觀察研究發現,某種魚群洄游的路線是曲線![]() ,曾有漁船在距
,曾有漁船在距![]() 島、
島、![]() 島距離和為8海里處發出過魚群。以
島距離和為8海里處發出過魚群。以![]() 所在直線為
所在直線為![]() 軸,
軸,![]() 的垂直平分線為
的垂直平分線為![]() 軸建立平面直角坐標系.
軸建立平面直角坐標系.
(1)求曲線![]() 的標準方程;
的標準方程;
(2)某日,研究人員在![]() 兩島同時用聲納探測儀發出不同頻率的探測信號(傳播速度相同),
兩島同時用聲納探測儀發出不同頻率的探測信號(傳播速度相同),![]() 兩島收到魚群在
兩島收到魚群在![]() 處反射信號的時間比為
處反射信號的時間比為![]() ,問你能否確定
,問你能否確定![]() 處的位置(即點
處的位置(即點![]() 的坐標)?
的坐標)?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于曲線![]() 所在的平面上的定點
所在的平面上的定點![]() ,若存在以點
,若存在以點![]() 為頂點的角
為頂點的角![]() ,使得
,使得![]() 對于曲線
對于曲線![]() 上的任意兩個不同的點
上的任意兩個不同的點![]() 恒成立,則稱角
恒成立,則稱角![]() 為曲線
為曲線![]() 的“
的“![]() 點視角”,并稱其中最小的“
點視角”,并稱其中最小的“![]() 點視角”為曲線
點視角”為曲線![]() 相對于點
相對于點![]() 的”
的”![]() 點確視角”.已知曲線
點確視角”.已知曲線![]() 和圓
和圓![]() 是
是![]() 軸上一點
軸上一點
(1)對于坐標原點![]() ,寫出曲線
,寫出曲線![]() 的“
的“![]() 點確視角”的大小;
點確視角”的大小;
(2)若![]() 在曲線
在曲線![]() 上,求
上,求![]() 的最小值;
的最小值;
(3)若曲線![]() 和圓
和圓![]() 的“
的“![]() 點確視角”相等,求
點確視角”相等,求![]() 點坐標.
點坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】七巧板是古代中國勞動人民發明的一種中國傳統智力玩具,它由五塊等腰直角三角形,一塊正方形和一塊平行四邊形共七塊板組成.清陸以湉《冷廬雜識》卷一中寫道:近又有七巧圖,其式五,其數七,其變化之式多至千余.體物肖形,隨手變幻,蓋游戲之具,足以排悶破寂,故世俗皆喜為之.如圖是一個用七巧板拼成的正方形,若在此正方形中任取一點,則此點取自陰影部分的概率為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com