【題目】設集合 
，則A∩（RB）等于（ ）
A.（﹣∞，1）
B.（0，4）
C.（0，1）
D.（1，4）
【答案】C
【解析】解：當x＞0時，A中不等式變形得x＜1，此時0＜x＜1；
當x＜0時，A中不等式變形得：x＞1，此時無解，
∴A=（0，1），
由B中y= 
，得到2x﹣16≥0，即2x≥24 ，
解得：x≥4，即B=[4，+∞），
∴RB=（﹣∞，4），
則A∩（RB）=（0，1），
故選：C．
【考點精析】利用交、并、補集的混合運算對題目進行判斷即可得到答案，需要熟知求集合的并、交、補是集合間的基本運算，運算結果仍然還是集合，區分交集與并集的關鍵是“且”與“或”，在處理有關交集與并集的問題時，常常從這兩個字眼出發去揭示、挖掘題設條件，結合Venn圖或數軸進而用集合語言表達，增強數形結合的思想方法．
口算題卡加應用題集訓系列答案科目：高中數學 來源： 題型：
【題目】據某市供電公司數據，2019年1月份市新能源汽車充電量約270萬度，同比2018年增長
，為了增強新能源汽車的推廣運用，政府加大了充電樁等基礎設施的投入.現為了了解該城市充電樁等基礎設施的使用情況，隨機選取了200個駕駛新能源汽車的司機進行問卷調查，根據其滿意度評分值（百分制）按照
，
，…，
分成5組，制成如圖所示的頻率分布直方圖.
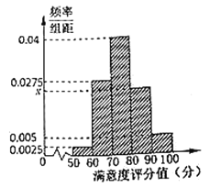
（1）求圖中
的值并估計樣本數據的中位數；
（2）已知滿意度評分值在內的男女司機人數比為
，從中隨機抽取2人進行座談，求2人均為女司機的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4﹣4：極坐標與參數方程
極坐標系與直角坐標系xOy有相同的長度單位，以原點O為極點，以x軸正半軸為極軸．已知曲線C1的極坐標方程為 
，曲線C2的極坐標方程為ρsinθ=a（a＞0），射線 
， 
與曲線C1分別交異于極點O的四點A，B，C，D．
（Ⅰ）若曲線C1關于曲線C2對稱，求a的值，并把曲線C1和C2化成直角坐標方程；
（Ⅱ）求|OA||OC|+|OB||OD|的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】從某工廠生產線上隨機抽取16件零件，測量其內徑數據從小到大依次排列如下（單位：
）：1.12，1.15，1.21，1.23，1.25，1.25，1.26，1.30，1.30，1.32，1.34，1.35，1.37，1.38，1.41，1.42，據此可估計該生產線上大約有25%的零件內徑小于等于_____，大約有30%的零件內徑大于_____．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的離心率為
，以原點為圓心，橢圓的短半軸長為半徑的圓與直線
相切．
（1）求橢圓
的方程；
（2）設點
是軌跡上位于第一象限且在直線
右側的動點，若以為圓心，線段
為半徑的圓與
有兩個公共點．試求圓在右焦點
處的切線
與軸交點縱坐標的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數 
（其中ω＞0），若f（x）的一條對稱軸離最近的對稱中心的距離為 
．
（1）求y=f（x）的單調遞增區間；
（2）在△ABC中角A、B、C的對邊分別是a，b，c滿足（2b﹣a）cosC=ccosA，則f（B）恰是f（x）的最大值，試判斷△ABC的形狀．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓 
（a＞b＞0）的左、右焦點分別為F1 ， F2 ， 過F1且與x軸垂直的直線交橢圓于A、B兩點，直線AF2與橢圓的另一個交點為C，若△ABF2的面積是△BCF2的面積的2倍，則橢圓的離心率為（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知拋物線x2=y，點A（﹣ 
， 
），B（ 
， 
），拋物線上的點P（x，y）（﹣ ＜x＜ ），過點B作直線AP的垂線，垂足為Q．
（Ⅰ）求直線AP斜率的取值范圍；
（Ⅱ）求|PA||PQ|的最大值．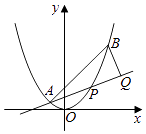
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
