
【題目】某廠商為了解用戶對其產品是否滿意,在使用產品的用戶中隨機調查了80人,結果如下表:
(1)根據上述,現用分層抽樣的方法抽取對產品滿意的用戶5人,在這5人中任選2人,求被選中的恰好是男、女用戶各1人的概率;
(2)有多大把握認為用戶對該產品是否滿意與用戶性別有關?請說明理由.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
注: ![]()
【答案】
(1)解:在滿意產品的女用戶中應抽取20× ![]() =2(人)記r,s
=2(人)記r,s
在滿意產品的男用戶中應抽取30× ![]() =3(人)記a,b,c
=3(人)記a,b,c
從5人中任選2人,共有10種情況:ab,ac,ar,as,bc,br,bs,cr,cs,rs
其中一男一女的情況6種,所以P= ![]() =
= ![]()
(2)解:K2= ![]() ≈5.333>5.024
≈5.333>5.024
所以有97.5%的把握認為用戶對該產品是否滿意與用戶性別有關
【解析】(1)根據分層抽樣原理,計算應抽取的女生、男生人數,用列舉法計算出基本事件的個數進而得出所求事件的概率。(2)計算出K2 的值,再對照臨界值即可得出結論。
【考點精析】認真審題,首先需要了解分層抽樣(先將總體中的所有單位按照某種特征或標志(性別、年齡等)劃分成若干類型或層次,然后再在各個類型或層次中采用簡單隨機抽樣或系用抽樣的辦法抽取一個子樣本,最后,將這些子樣本合起來構成總體的樣本).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】設![]() 是異面直線,則以下四個命題:①存在分別經過直線
是異面直線,則以下四個命題:①存在分別經過直線![]() 和
和![]() 的兩個互相垂直的平面;②存在分別經過直線
的兩個互相垂直的平面;②存在分別經過直線![]() 和
和![]() 的兩個平行平面;③經過直線
的兩個平行平面;③經過直線![]() 有且只有一個平面垂直于直線
有且只有一個平面垂直于直線![]() ;④經過直線
;④經過直線![]() 有且只有一個平面平行于直線
有且只有一個平面平行于直線![]() ,其中正確的個數有( )
,其中正確的個數有( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】電商中“貓狗大戰”在節日期間的競爭異常激烈,在剛過去的618全民年中購物節中,某東當日交易額達1195億元,現從該電商“剁手黨”中隨機抽取100名顧客進行回訪,按顧客的年齡分成了6組,得到如下所示的頻率直方圖. 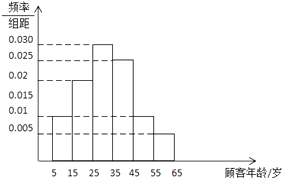
(1)求顧客年齡的眾數,中位數,平均數(每一組數據用中點做代表);
(2)用樣本數據的頻率估計總體分布中的概率,則從全部顧客中任取3人,記隨機變量X為顧客中年齡小于25歲的人數,求隨機變量X的分布列以及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)(sinx+cosx)2+2cos2x﹣2
(1)求函數f(x)的最小正周期T;
(2)求f(x)的最大值,并指出取得最大值時x取值集合;
(3)當x∈[ ![]() ,
, ![]() ]時,求函數f(x)的值域.
]時,求函數f(x)的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校從6名學生會干部(其中男生4人,女生2人)中選3人參加青年聯合會志愿者。
(1)設所選3人中女生人數為 ![]() ,求
,求 ![]() 的分布列及數學期望;
的分布列及數學期望;
(2)在男生甲被選中的情況下,求女生乙也被選中的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】平面直角坐標系 ![]() 中,過橢圓
中,過橢圓 ![]() :
: ![]() (
( ![]() )右焦點的直線
)右焦點的直線 ![]() 交
交 ![]() 于
于 ![]() ,
, ![]() 兩點,
兩點, ![]() 為
為 ![]() 的中點,且
的中點,且 ![]() 的斜率為
的斜率為 ![]() .
.
(Ⅰ)求橢圓 ![]() 的方程;
的方程;
(Ⅱ) ![]() ,
, ![]() 為
為 ![]() 上的兩點,若四邊形
上的兩點,若四邊形 ![]() . 的對角線
. 的對角線 ![]() ,求四邊形
,求四邊形 ![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知三棱柱![]() 的所有棱長都相等,且側棱垂直于底面,由
的所有棱長都相等,且側棱垂直于底面,由![]() 沿棱柱側面經過棱
沿棱柱側面經過棱![]() 到點
到點![]() 的最短路線長為
的最短路線長為![]() ,設這條最短路線與
,設這條最短路線與![]() 的交點為
的交點為![]() .
.

(1)求三棱柱![]() 的體積;
的體積;
(2)證明:平面![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 為奇函數,
為奇函數, ![]() 為常數.
為常數.
(1)確定![]() 的值;
的值;
(2)求證: ![]() 是
是![]() 上的增函數;
上的增函數;
(3)若對于區間![]() 上的每一個
上的每一個![]() 值,不等式
值,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com