日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情

【題目】已知點A,B,C,D是直角坐標系中不同的四點，若，，且，則下列說法正確的是( ),

A.C可能是線段AB的中點

B.D可能是線段AB的中點

C.C、D可能同時在線段AB上

D.C、D不可能同時在線段AB的延長線上

【答案】D

【解析】

根據向量共線定理得到四點共線，再根據反證法求證，問題可逐一解決.

解：由，，可得：四點共線，

對于選項A，若C是線段AB的中點，則，則，不滿足，即選項A錯誤；

對于選項B，若D是線段AB的中點，則，則，不滿足，即選B錯誤；

對于選項C，若C、D同時在線段AB上，則，則，不滿足，即選項C錯誤；

對于選項D，假設C、D同時在線段AB的延長線上，則 ，則，則不滿足，即假設不成立，即C、D不可能同時在線段AB的延長線上，即選項D正確；

故選：D.

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

【題目】前些年有些地方由于受到提高的影響，部分企業只重視經濟效益而沒有樹立環保意識，把大量的污染物排放到空中與地下，嚴重影響了人們的正常生活，為此政府進行強制整治，對不合格企業進行關閉、整頓，另一方面進行大量的綠化來凈化和吸附污染物.通過幾年的整治，環境明顯得到好轉，針對政府這一行為，老百姓大大點贊.

（1）某機構隨機訪問50名居民，這50名居民對政府的評分（滿分100分）如下表：

分數

頻數

2

3

11

14

11

9

請在答題卡上作出居民對政府的評分頻率分布直方圖：

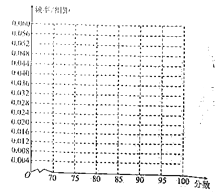
（2）當地環保部門隨機抽測了2018年11月的空氣質量指數，其數據如下表：

空氣質量指數（）

0-50

50-100

100-150

150-200

天數

2

18

8

2

用空氣質量指數的平均值作為該月空氣質量指數級別，求出該月空氣質量指數級別為第幾級？（同一組數據用該組數據的區間中點值作代表，將頻率視為概率）（相關知識參見附表）

（3）空氣受到污染，呼吸系統等疾病患者最易感染，根據歷史經驗，凡遇到空氣輕度污染，小李每天會服用有關藥品，花費50元，遇到中度污染每天服藥的費用達到100元.環境整治前的2015年11月份小李因受到空氣污染患呼吸系統等疾病花費了5000元，試估計2018年11月份（參考（2）中表格數據）小李比以前少花了多少錢的醫藥費？

附：

空氣質量指數（）

0-50

50-100

100-150

150-200

200-300

空氣質量指數級別

Ⅰ

Ⅱ

Ⅲ

Ⅳ

Ⅴ

Ⅵ

空氣質量指數

優

良

輕度污染

中度污染

重度污染

嚴重污染

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】如圖，已知棱柱的底面是菱形，且面ABCD，，F為棱的中點，M為線段的中點．

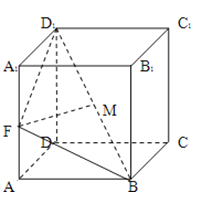
（1）求證：面ABCD；

（2）判斷直線MF與平面的位置關系，并證明你的結論；

（3）求三棱錐的體積．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】為改善人居環境，某區增加了對環境綜合治理的資金投入，已知今年治理環境（畝）與相應的資金投入（萬元）的四組對應數據的散點圖如圖所示，用最小二乘法得到關于的線性回歸方程.

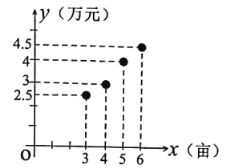
（1）求的值，并預測今年治理環境10畝所需投入的資金是多少萬元？

（2）已知該區去年治理環境10畝所投入的資金為3.5萬元，根據（1）的結論，請你對該區環境治理給出一條簡短的評價.

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】在梯形中，，為的中點，線段與交于點（如圖1）.將沿折起到的位置，使得二面角為直二面角（如圖2）.

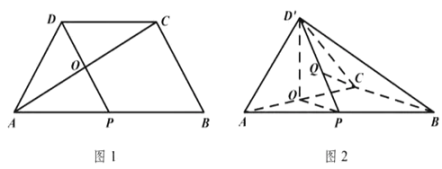
（1）求證：平面；

（2）線段上是否存在點，使得與平面所成角的正弦值為？若存在，求出的值；若不存在，請說明理由.

查看答案和解析>>

科目：高中數學 來源： 題型：

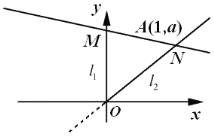
【題目】如圖，設直線：，：.點的坐標為.過點的直線的斜率為，且與，分別交于點，（，的縱坐標均為正數）.

（1）求實數的取值范圍；

（2）設，求面積的最小值；

（3）是否存在實數，使得的值與無關?若存在，求出所有這樣的實數；若不存在，說明理由.

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】我市為增強市民的環境保護意識，面向全市征召義務宣傳志愿者.現從符合條件的志愿者中隨機抽取100名按年齡（單位：歲）分組：第1組，第2組，第3組，第4組，第5組，得到的頻率分布直方圖如圖所示.

（1）若從第3，4，5組中用分層抽樣的方法抽取6名志愿者參加廣場的宣傳活動，應從第3，4，5組各抽取多少名志愿者？

（2）請根據頻率分布直方圖，估計這100名志愿者樣本的平均數；

（3）在（1）的條件下，該市決定在這6名志愿者中隨機抽取2名志愿者介紹宣傳經驗，求第4組至少有一名志愿者被抽中的概率.（參考數據： ）

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知橢圓（）的左右焦點分別為，，已知其離心率為，且過點.

（1）求橢圓的標準方程.

（2）設，是橢圓上位于軸上方的兩點，且直線與直線平行，與交于點，探究是否為定值？如果為定值，請求出該定值；如果不為定值，請說明理由.

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】新個稅法于2019年1月1日進行實施.為了調查國企員工對新個稅法的滿意程度，研究人員在地各個國企中隨機抽取了1000名員工進行調查，并將滿意程度以分數的形式統計成如下的頻率分布直方圖，其中.

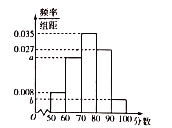
（1）求的值并估計被調查的員工的滿意程度的中位數；（計算結果保留兩位小數）

（2）若按照分層抽樣從，中隨機抽取8人，再從這8人中隨機抽取2人，求至少有1人的分數在的概率.

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 国产欧美精品一区二区三区四区 | 国产suv精品一区二区33 | 国产精品美女久久久久久久网站 | 国产成人午夜 | 国产精品亚洲综合 | 日韩中文字幕一区二区 | 黄色一级免费电影 | 中文在线 | 中文 | 国产一区二区三区视频在线观看 | 久久成人一区 | 91久久国产综合久久91精品网站 | 久久首页 | 午夜视频黄 | 亚洲黄色在线免费观看 | 欧美激情视频免费观看 | 亚洲日本欧美日韩高观看 | 欧美精品一区在线发布 | 久久国产精品99久久久久久老狼 | 男女视频在线观看 | 国产精品免费视频观看 | 日韩av电影观看 | 精品在线一区二区 | 欧美在线综合视频 | 麻豆精品一区二区 | 亚洲第一视频 | 成人一级毛片 | av青青| 欧美成人黑人xx视频免费观看 | 国产精品久久一区二区三区 | 亚洲精品国产精品乱码不99按摩 | 中文字幕欧美日韩一区 | 一区二区三区四区在线 | 亚洲视频在线观看网站 | 日韩手机在线视频 | 中文字幕在线乱码不卡二区区 | 国产精品美女久久久久久久久久久 | 日本特黄| 精品国产欧美一区二区三区成人 | 天天天天天天天天干 | 日韩精品第一页 | 精品日韩一区二区 |