解:(1)f
1(x),f
2(x)是“三角形函數”,f
3(x)不是“三角形函數”.
任給三角形,設它的三邊長分別為a,b,c,則a+b>c,不妨假設a≤c,b≤c,
由于
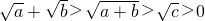
,所以f
1(x),f
2(x)是“保三角形函數”.
對于f
3(x),3,3,5可作為一個三角形的三邊長,但3
2+3
2<5
2,
所以不存在三角形以3
2,3
2,5
2為三邊長,故f
3(x)不是“保三角形函數”.
(2)設T>0為g(x)的一個周期,由于其值域為(0,+∞),
所以,存在n>m>0,使得g(m)=1,g(n)=2,
取正整數
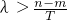
,可知λT+m,λT+m,n這三個數可作為一個三角形的三邊長,
但g(λT+m)=1,g(λT+m)=1,g(n)=2不能作為任何一個三角形的三邊長.
故g(x)不是“三角形函數”.
(3)當
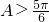
,
取
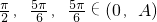
,顯然這三個數可作為一個三角形的三邊長,
但
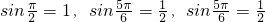
不能作為任何一個三角形的三邊長,
故F(x)不是“三角形函數”.
分析:(1)任給三角形,設它的三邊長分別為a,b,c,則a+b>c,不妨假設a≤c,b≤c,我們判斷f(a),f(b),f(c)是否滿足任意兩數之和大于第三個數,即任意兩邊之和大于第三邊;
(2)要想一個函數不是“三角形函數”關鍵是根據題中條件g(x)是定義在R上的周期函數,且值域為(0,+∞),舉出反例;
(3)當
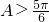
,取
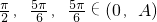
,顯然這三個數可作為一個三角形的三邊長,但
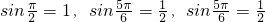
不能作為任何一個三角形的三邊長,最后給出結論.
點評:本小題主要考查進行簡單的合情推理、三角函數的性質等基礎知識,考查運算求解能力,考查化歸與轉化思想.要想判斷f(x)為“三角形函數”,要經過嚴密的論證說明f(x)滿足“三角形函數”的概念,但要判斷f(x)不為“三角形函數”,僅須要舉出一個反例即可.

 ,f2(x)=x,f3(x)=x2中,哪些是“三角形函數”,哪些不是,并說明理由;
,f2(x)=x,f3(x)=x2中,哪些是“三角形函數”,哪些不是,并說明理由; 時,F(x)不是“三角形函數”.
時,F(x)不是“三角形函數”.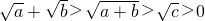 ,所以f1(x),f2(x)是“保三角形函數”.
,所以f1(x),f2(x)是“保三角形函數”.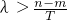 ,可知λT+m,λT+m,n這三個數可作為一個三角形的三邊長,
,可知λT+m,λT+m,n這三個數可作為一個三角形的三邊長,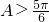 ,
,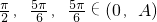 ,顯然這三個數可作為一個三角形的三邊長,
,顯然這三個數可作為一個三角形的三邊長,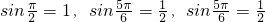 不能作為任何一個三角形的三邊長,
不能作為任何一個三角形的三邊長,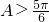 ,取
,取 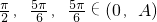 ,顯然這三個數可作為一個三角形的三邊長,但
,顯然這三個數可作為一個三角形的三邊長,但 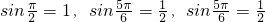 不能作為任何一個三角形的三邊長,最后給出結論.
不能作為任何一個三角形的三邊長,最后給出結論.

 科學實驗活動冊系列答案
科學實驗活動冊系列答案 ,f2(x)=x,f3(x)=x2中,哪些是“三角形函數”,哪些不是,并說明理由;
,f2(x)=x,f3(x)=x2中,哪些是“三角形函數”,哪些不是,并說明理由; 時,F(x)不是“三角形函數”.
時,F(x)不是“三角形函數”.