
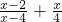 .
.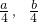 ],若存在,求實數a、b的值;若不存在,說明理由.
],若存在,求實數a、b的值;若不存在,說明理由.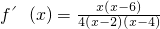 .注意到
.注意到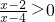 ,即x∈(-∞,2)∪(4,+∞),
,即x∈(-∞,2)∪(4,+∞),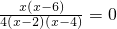 得x=6或x=0.所以當x變化時,f′(x),f(x)的變化情況如下表:
得x=6或x=0.所以當x變化時,f′(x),f(x)的變化情況如下表: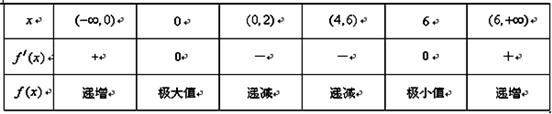
 是f(x)的一個極大值,f(6)=ln2+
是f(x)的一個極大值,f(6)=ln2+ 是f(x)的一個極大值..
是f(x)的一個極大值.. ),所以f(x)的圖象的對稱中心只可能是(3,
),所以f(x)的圖象的對稱中心只可能是(3, ).
). )對稱,只需證明點Q也在y=f(x)上,即證y0=f(x0)
)對稱,只需證明點Q也在y=f(x)上,即證y0=f(x0) )的對稱點是Q(x0,y0),
)的對稱點是Q(x0,y0),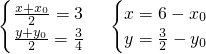 ,又
,又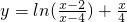
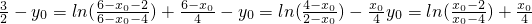 ,
, <0,而
<0,而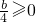 ∴
∴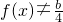 .故不可能…
.故不可能… >
> ,而
,而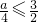 ∴f(x)≠
∴f(x)≠ .故不可能….
.故不可能…. 的兩個解.而f(x)-
的兩個解.而f(x)- =
=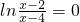 無解.故此時f的取值范f(x)圍是不可能是[
無解.故此時f的取值范f(x)圍是不可能是[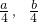 ].
]. ),所以f(x)的圖象的對稱中心只可能是(3,
),所以f(x)的圖象的對稱中心只可能是(3, ).方程(曲線)觀點要證f(x)的圖象關于(3,
).方程(曲線)觀點要證f(x)的圖象關于(3, )對稱,只需證明點Q也在y=f(x)上,即證y0=f(x0)即可.
)對稱,只需證明點Q也在y=f(x)上,即證y0=f(x0)即可.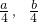 ].因而滿足條件的實數a、b不存在.
].因而滿足條件的實數a、b不存在.

科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| 2(x-1) |
| x+1 |
| x1+x2 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| f(n) |
查看答案和解析>>
科目:高中數學 來源: 題型:
| ||
| a |
| ||
| x |
| 6 |
| 6 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com