
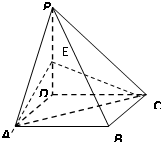
 如圖,四棱錐P-ABCD是底面邊長為1的正方形,PD⊥BC,PD=1,PC=
如圖,四棱錐P-ABCD是底面邊長為1的正方形,PD⊥BC,PD=1,PC=| 2 |
| 2 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |


科目:高中數學 來源: 題型:
 如圖,四棱錐P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如圖,四棱錐P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,四棱錐P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,側面PAD⊥底面ABCD,且△PAD為等腰直角三角形,∠APD=90°,M為AP的中點.
如圖,四棱錐P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,側面PAD⊥底面ABCD,且△PAD為等腰直角三角形,∠APD=90°,M為AP的中點.查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,四棱錐P-ABCD的底面ABCD是矩形,AB=2,BC=
如圖,四棱錐P-ABCD的底面ABCD是矩形,AB=2,BC=| 2 |
| AE |
| AP |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,四棱錐P-ABCD中,底面ABCD為矩形,PA⊥底面ABCD,且PA=AB=1,AD=
如圖,四棱錐P-ABCD中,底面ABCD為矩形,PA⊥底面ABCD,且PA=AB=1,AD=| 3 |
| ||
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,四棱錐P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=2
如圖,四棱錐P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=2| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com