日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情

【題目】已知集合A={x|3≤3x≤27}，B={x|log2x＞1}．

（1）分別求A∩B，（RA）∪（RB）；

（2）已知集合C={x|a＜x＜a2+1}，若CA，求滿足條件的實數a的取值范圍．

【答案】（1）A∩B=（2，3], （RA）∪（RB）=（-∞，2]∪（3，+∞）（2）

【解析】

（1）先求出集合A，B，然后進行交、并、補的運算即可；

（2）因為CA，所以分C=，和C≠兩種情況，然后分別求a在這兩種情況下的取值，再取并集即可．

解：（1）A=[1，3]，B=（2，+∞）；

∴A∩B=（2，3]，RA=（-∞，1）∪（3，+∞），RB=（-∞，2]，

（RA）∪（RB）=（-∞，2]∪（3，+∞）；

（2）∵CA，∴若C=，則a≥a2+1，解得a∈；

若C≠，則，解得1；

∴實數a的取值范圍為．

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

【題目】函數f（x）=是定義在R上的奇函數，且f（1）=1．

（1）求a，b的值；

（2）判斷并用定義證明f（x）在（+∞）的單調性．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知：如圖，梯形ABCD中，AD∥BC，∠C= ，以AB為直徑的⊙O恰與CD相切于點E，⊙O交BC于F，連結EF．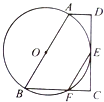

（1）求證：AD+BC=AB；
（2）求證：EF是AD與AB的等比中項．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】設:實數滿足,其中;

:實數滿足.

（Ⅰ）若,且為真,求實數的取值范圍;

（Ⅱ）若是的必要不充分條件,求實數的取值范圍.

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知函數f（x）=（x+1）2ex ， 設k∈[﹣3，﹣1]，對任意x1 ， x2∈[k，k+2]，則|f（x1）﹣f（x2）|的最大值為（ ）
A.4e﹣3
B.4e
C.4e+e﹣3
D.4e+1

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知函數對一切實數都有 成立，且.

（1）求的值；

（2）求的解析式；

（3）已知，設：當時，不等式 恒成立；Q：當時，是單調函數。如果滿足成立的的集合記為，滿足Q成立的的集合記為，求A∩(CRB)（為全集）．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知函數f（x）=bx﹣axlnx（a＞0）的圖象在點（1，f（1））處的切線與直線平y=（1﹣a）x行．
（1）若函數y=f（x）在[e，2e]上是減函數，求實數a的最小值；
（2）設g（x）= ，若存在x1∈[e，e2]，使g（x1）≤ 成立，求實數a的取值范圍．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】在極坐標系中，已知某曲線C的極坐標方程為，直線的極坐標方程為

（1）求該曲線C的直角坐標系方程及離心率

（2）已知點為曲線C上的動點，求點到直線的距離的最大值。

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知函數f(x)=lnx - .

(1)求函數f(x)的單調遞增區間;

(2)證明:當x>1時,f(x)<x-1;

(3)確定實數k的所有可能取值,使得存在x0>1,當x∈(1,x0)時,恒有f(x)>k(x-1).

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 国产精品大片在线观看 | 99精品全国免费观看视频软件 | 亚洲成人精品在线观看 | 欧美精品成人在线视频 | 久久伊人精品视频 | 国产一区二区在线电影 | 日韩伦理一区二区三区 | 国产中文在线播放 | 亚洲高清av在线 | 国产精品久久久久久久久免费 | 国产成人免费 | 国偷自产av一区二区三区 | 成人免费高清视频 | 国产日韩欧美在线观看 | 一区二区三区国产精品 | 亚洲电影中文字幕 | 激情999| 亚洲欧美另类图片 | 中文字幕91 | 日本一区二区不卡视频 | 成人一区电影 | 成人精品一区二区三区中文字幕 | 国产一区二区三区不卡在线观看 | 黄色影院免费看 | 看欧美黄色录像 | 欧美日韩一二三 | 国产v日产∨综合v精品视频 | 精品一区二区免费视频 | 欧美日批| 欧美精品成人 | 男女靠逼免费视频 | 欧美午夜精品一区二区三区电影 | 狠狠做深爱婷婷综合一区 | 精品视频99| 久久精品国产免费 | 中文字幕av在线播放 | 色视频网站在线观看一=区 www..99re | 北条麻妃99精品青青久久 | 精一区二区 | 欧美日韩二区三区 | 黄色一级片在线观看 |