【題目】如圖，四棱錐
的底面
是直角梯形,
,
,側面
底面,
是等邊三角形，
，點
分別是棱
的中點 .
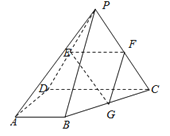
（Ⅰ）求證：
平面
；
（Ⅱ）求二面角
的大小；
（Ⅲ）在線段
上存在一點
，使
平面
，且
，求
的值.
【答案】(1)詳見解析;(2) 
;(3) 
.
【解析】
試題
(Ⅰ)由題意證得
，結合線面平行的判斷定理可得
平面
.
(Ⅱ)建立空間直角坐標系，結合平面的法向量可得二面角
的大小為30°；
(Ⅲ)利用(II)中的空間直角坐標系結合空間向量的坐標表示得到關于實數
的方程，解方程可得.
試題解析：
（Ⅰ）證明：設
是
的中點，連接
∵ 
分別是
的中點
∴ 
，
，∴
∴ 
四點共面
∵ ，
平面
，∴平面
（Ⅱ）
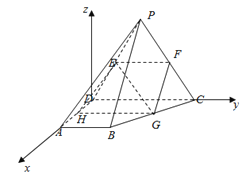
∵ 平面
底面，
∴ 
平面，過點
作
軸與平面
垂直，則軸
平面
以
分別為
軸，
軸建立空間直角坐標系
設平面
的法向量為
，則
設平面的法向量為
，
，
，
，
∴
∴ 
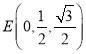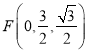
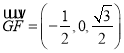
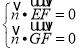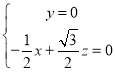
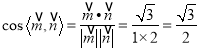
，∴所求二面角大小為.
（Ⅲ）
，
，
，
，設
，
，
∴ 
，
∵ 
平面
，∴
∴ 
， .
雙基同步導航訓練系列答案
黃岡小狀元同步計算天天練系列答案科目：高中數學 來源： 題型：
【題目】各項均為正數的數列
的前
項和為
，且對任意正整數，都有
．
（1）求數列的通項公式；
（2）如果等比數列
共有2016項，其首項與公比均為2，在數列的每相鄰兩項
與
之間插入
個
后，得到一個新的數列
．求數列中所有項的和；
（3）是否存在實數
，使得存在
，使不等式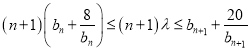
成立，若存在，求實數的范圍，若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，其中
.
（1）若曲線
在點
處的切線與直線
平行，求
與
滿足的關系；
（2）當
時，討論
的單調性；
（3）當
時，對任意的
，總有
成立，求實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，
是橢圓
：
上的點，過點
的直線的方程為
.
（1）求橢圓的離心率；
（2）當
時，
（i）設直線
與
軸、
軸分別相交于
，
兩點，求
的最小值；
（ii）設橢圓的左、右焦點分別為
，
，點
與點關于直線對稱，求證：點，，三點共線.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
： 
的離心率為
，橢圓的四個頂點圍成的四邊形的面積為4.
（Ⅰ）求橢圓
的標準方程；
（Ⅱ）直線
與橢圓
交于
， 
兩點， 
的中點
在圓
上，求
（
為坐標原點）面積的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】車間將10名技工平均分成甲乙兩組加工某種零件,在單位時間內每個技工加工的合格零件數的統計數據的莖葉圖如圖所示.已知兩組技工在單位時間內加工的合格零件平均數都為10.
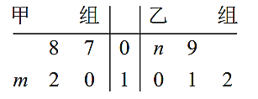
(1)分別求出
,
的值;
(2)質檢部門從該車間甲乙兩組技工中各隨機抽取一名技工,對其加工的零件進行檢測,若兩人加工的合格零件個數之和大于17,則稱該車間“質量合格”,求該車間“質量合格”的概率;
(3)根據以上莖葉圖和你所學的統計知識,分析兩組技工的整體加工水平及穩定性.
(注:方差
,其中
為數據
,
,…,
的平均數).
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】謝爾賓斯基三角形（Sierpinskitriangle）是一種分形幾何圖形，由波蘭數學家謝爾賓斯基在1915年提出，它是一個自相似的例子，其構造方法是：
（1）取一個實心的等邊三角形（圖1）；
（2）沿三邊中點的連線，將它分成四個小三角形；
（3）挖去中間的那一個小三角形（圖2）；
（4）對其余三個小三角形重復（1）（2）（3）（4）（圖3）.
制作出來的圖形如圖4，圖5，….
若圖3（陰影部分）的面積為1，則圖5（陰影部分）的面積為（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】【選修4-4，坐標系與參數方程】
在直角坐標系
中，直線
的參數方程為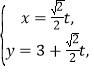
（t為參數），在以O為極點，
軸正半軸為極軸的極坐標系中，曲線C的極坐標方程為
（Ⅰ）求直線的普通方程與曲線C的直角坐標方程；
（Ⅱ）若直線與
軸的交點為P，直線與曲線C的交點為A,B,求
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
