
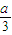 )(x+a)
)(x+a)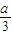 <-a
<-a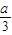 )、(-a,+∞)上單調遞增,在(
)、(-a,+∞)上單調遞增,在(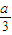 ,-a)上單調遞減(4分)
,-a)上單調遞減(4分)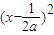 -
-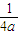 -1,
-1,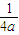 -1(-1≤a<0)(10分)
-1(-1≤a<0)(10分)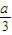 )、(-a,+∞)上單調遞增,
)、(-a,+∞)上單調遞增,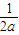 )上單調遞增
)上單調遞增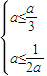 得a≤-
得a≤-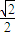 (12分)
(12分)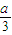 ,+∞)上單調遞增,
,+∞)上單調遞增,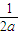 ,+∞)上單調遞增
,+∞)上單調遞增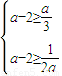 得a≥3
得a≥3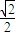 ]∪[3,+∞)(13分)
]∪[3,+∞)(13分)

 舉一反三單元同步過關卷系列答案
舉一反三單元同步過關卷系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| 4x |
| x2+a |
| x | 0 | 0.1 | 0.2 | 0.5 | 0.8 | 1 | 1.2 | 1.5 | 1.8 | 2 | 4 | 6 | … |
| y | 0 | 0.396 | 0.769 | 1.6 | 1.951 | 2 | 1.967 | 1.846 | 1.698 | 1.6 | 0.941 | 0.649 | … |
| 4x |
| x2+a |
| 3 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com