
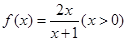
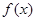 在
在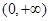 上為單調增函數;
上為單調增函數;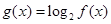 ,求
,求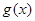 的值域;
的值域; 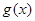 ,若關于
,若關于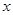 的方程
的方程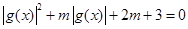 有三個不同的實數解,求
有三個不同的實數解,求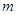 的取值范圍.
的取值范圍.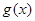 值域為
值域為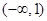 ;(3)
;(3)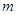 的取值范圍為
的取值范圍為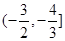 。
。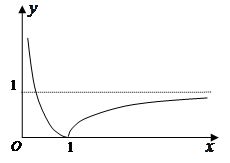
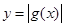 可知其圖像,然后徐結合圖像,
可知其圖像,然后徐結合圖像,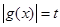 ,則
,則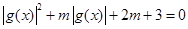 有三個不同的實數解,即為
有三個不同的實數解,即為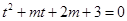 有兩個根,且一個在
有兩個根,且一個在 上,一個在
上,一個在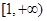 上,然后分析得到m的范圍。
上,然后分析得到m的范圍。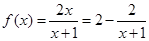 ,設
,設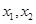 是
是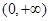 上的任意兩個數,且
上的任意兩個數,且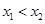 ,……2分
,……2分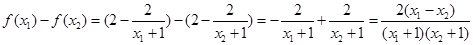 ……4分
……4分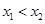 ,∴
,∴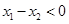 ,∴
,∴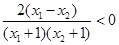 即
即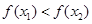
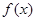 在
在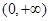 上為增函數, …………………………6分
上為增函數, …………………………6分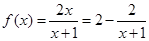 ,
,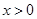 ,所以
,所以 ,所以
,所以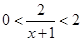 ,
,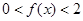 …………………………8分
…………………………8分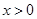 時,
時,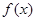 單調遞增,
單調遞增,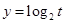 單調遞增,
單調遞增,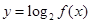 單調遞增,所以
單調遞增,所以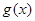 值域為
值域為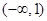 …………………………10分
…………………………10分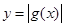 大致圖象如右圖所示,
大致圖象如右圖所示,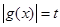 ,則
,則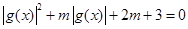 有三個不同的實數解,即為
有三個不同的實數解,即為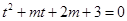 有兩個根,且一個在
有兩個根,且一個在 上,一個在
上,一個在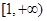 上,設
上,設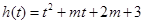 ………12分
………12分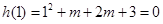 ,
,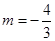 ,此時另一根為
,此時另一根為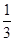 適合題意; ………………13分
適合題意; ………………13分 ,得
,得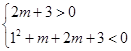 ,∴
,∴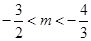
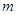 的取值范圍為
的取值范圍為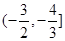 …………………………16分
…………………………16分

科目:高中數學 來源:不詳 題型:填空題
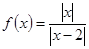 為偶函數; (2)函數
為偶函數; (2)函數 ;
;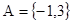 ,
,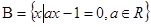 ,若
,若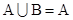 ,則實數
,則實數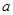 的取值集合為
的取值集合為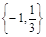 ; (4)集合
; (4)集合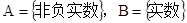 ,對應法則f:“求平方根”,則
,對應法則f:“求平方根”,則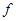 是A到B的映射;你認為正確命題的序號是 (把正確的序號都寫上).
是A到B的映射;你認為正確命題的序號是 (把正確的序號都寫上).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com