
【題目】已知二次函數(shù)![]() .
.
(Ⅰ)若![]() 的最大值為
的最大值為![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的值;
的值;
(Ⅱ)對(duì)于任意的![]() ,總有
,總有![]() .求實(shí)數(shù)
.求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
【答案】(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]()
【解析】
(Ⅰ) 設(shè)![]() ,
,![]() 轉(zhuǎn)化為二次函數(shù)
轉(zhuǎn)化為二次函數(shù)![]() 在
在![]() 的最值,由二次函數(shù)圖象性質(zhì)可知此最大值只能是
的最值,由二次函數(shù)圖象性質(zhì)可知此最大值只能是![]() 之一,通過(guò)討論,即可求出a;
之一,通過(guò)討論,即可求出a;
(Ⅱ)令t=sinxcosx,變量分離轉(zhuǎn)化為關(guān)于t的二次函數(shù)的最值,通過(guò)恒成立求出a的取值范圍.
解:(Ⅰ)二次函數(shù)中![]()
設(shè)![]() ∴
∴![]() ,若
,若![]() (
(![]() )的最大值為
)的最大值為![]()
即關(guān)于S的二次函數(shù)![]() 在區(qū)間上
在區(qū)間上![]() 有最大值
有最大值![]() ,
,
由二次函數(shù)圖象性質(zhì)可知此最大值只能是![]() 之一
之一
若![]() ,此時(shí)二次函數(shù)開(kāi)口向下且對(duì)稱軸
,此時(shí)二次函數(shù)開(kāi)口向下且對(duì)稱軸![]() ,所以函數(shù)在區(qū)間上最大值在頂點(diǎn)處取得,不是
,所以函數(shù)在區(qū)間上最大值在頂點(diǎn)處取得,不是![]() ,不合題意;
,不合題意;
若![]() ,此時(shí)二次函數(shù)開(kāi)口向上且對(duì)稱軸
,此時(shí)二次函數(shù)開(kāi)口向上且對(duì)稱軸![]() ,最大值
,最大值![]() ,符合題意
,符合題意
若![]() ,此時(shí)二次函數(shù)開(kāi)口向下且對(duì)稱軸
,此時(shí)二次函數(shù)開(kāi)口向下且對(duì)稱軸![]() ,并不在頂點(diǎn)處有最大值,不符合題意
,并不在頂點(diǎn)處有最大值,不符合題意
綜上所述![]() .
.
(Ⅱ)![]() 對(duì)于任意的
對(duì)于任意的![]() ,總有
,總有![]() ,
,
令![]() ,
,
則命題轉(zhuǎn)化為![]() ,不等式
,不等式![]() 恒成立,
恒成立,
當(dāng)![]() 時(shí),
時(shí),![]() 使
使![]() 成立;
成立;
當(dāng)![]() 時(shí),有
時(shí),有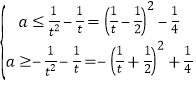
對(duì)于任意的![]() 恒成立;
恒成立;
∵![]() ∴
∴![]() 或
或![]() ,則
,則![]() ,故要使①式成立,
,故要使①式成立,
則有![]() ,又
,又![]() ,故要使②式成立,則有
,故要使②式成立,則有![]() ,由題設(shè)知
,由題設(shè)知![]() .
.
綜上,![]() 為所求。
為所求。



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)=|x﹣1|﹣2|x+1|的最大值為k.
(1)求k的值;
(2)若a,b,c∈R, ![]() +b2=k,求b(a+c)的最大值.
+b2=k,求b(a+c)的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)= ![]() ,g(x)=lnx,其中e為自然對(duì)數(shù)的底數(shù).
,g(x)=lnx,其中e為自然對(duì)數(shù)的底數(shù).
(1)求函數(shù)y=f(x)g(x)在x=1處的切線方程;
(2)若存在x1 , x2(x1≠x2),使得g(x1)﹣g(x2)=λ[f(x2)﹣f(x1)]成立,其中λ為常數(shù),求證:λ>e;
(3)若對(duì)任意的x∈(0,1],不等式f(x)g(x)≤a(x﹣1)恒成立,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某程序框圖如圖所示,該程序運(yùn)行后輸出的S的值是( ) 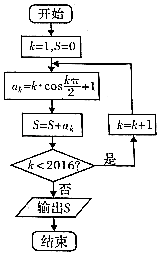
A.3024
B.1007
C.2015
D.2016
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】(本題滿分12分)全網(wǎng)傳播的融合指數(shù)是衡量電視媒體在中國(guó)網(wǎng)民中影響了的綜合指標(biāo).根據(jù)相關(guān)報(bào)道提供的全網(wǎng)傳播2015年某全國(guó)性大型活動(dòng)的“省級(jí)衛(wèi)視新聞臺(tái)”融合指數(shù)的數(shù)據(jù),對(duì)名列前20名的“省級(jí)衛(wèi)視新聞臺(tái)”的融合指數(shù)進(jìn)行分組統(tǒng)計(jì),結(jié)果如表所示.
組號(hào) | 分組 | 頻數(shù) |
1 |
| 2 |
2 |
| 8 |
3 |
| 7 |
4 |
| 3 |
(Ⅰ)現(xiàn)從融合指數(shù)在![]() 和
和![]() 內(nèi)的“省級(jí)衛(wèi)視新聞臺(tái)”中隨機(jī)抽取2家進(jìn)行調(diào)研,求至少有1家的融合指數(shù)在
內(nèi)的“省級(jí)衛(wèi)視新聞臺(tái)”中隨機(jī)抽取2家進(jìn)行調(diào)研,求至少有1家的融合指數(shù)在![]() 的概率;
的概率;
(Ⅱ)根據(jù)分組統(tǒng)計(jì)表求這20家“省級(jí)衛(wèi)視新聞臺(tái)”的融合指數(shù)的平均數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)=ln(x+a)﹣x,a∈R.
(1)當(dāng)a=﹣1時(shí),求f(x)的單調(diào)區(qū)間;
(2)若x≥1時(shí),不等式ef(x)+ ![]() x2>1恒成立,求實(shí)數(shù)a的取值范圍.
x2>1恒成立,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】下列說(shuō)法正確的是
A. 命題“若![]() ,則
,則![]() ”的否命題為“若
”的否命題為“若![]() ,則
,則![]() ”;
”;
B. 命題“![]() ”的否定是“
”的否定是“![]() ”;
”;
C. 命題“若x=y,則![]() ”的逆否命題為真命題;
”的逆否命題為真命題;
D. “![]() ” 是“
” 是“![]() ”的必要不充分條件.
”的必要不充分條件.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】直線y=kx﹣4,k>0與拋物線y2=2 ![]() x交于A,B兩點(diǎn),與拋物線的準(zhǔn)線交于點(diǎn)C,若AB=2BC,則k=( )
x交于A,B兩點(diǎn),與拋物線的準(zhǔn)線交于點(diǎn)C,若AB=2BC,則k=( )
A.![]()
B.![]()
C.2 ![]()
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在平面直角坐標(biāo)系xOy中,過(guò)點(diǎn)![]() 且互相垂直的兩條直線分別與圓
且互相垂直的兩條直線分別與圓![]() 交于點(diǎn)A,B,與圓
交于點(diǎn)A,B,與圓![]() 交于點(diǎn)C,D.
交于點(diǎn)C,D.

(1) 若AB=![]() ,求CD的長(zhǎng);
,求CD的長(zhǎng);
(2)若直線![]() 斜率為2,求
斜率為2,求![]() 的面積;
的面積;
(3) 若CD的中點(diǎn)為E,求△ABE面積的取值范圍.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com