Question

【題目】已知函數，.

（1）若函數的圖像與軸無交點，求的取值范圍；

（2）若方程在區間上存在實根，求的取值范圍；

（3）設函數，，當時若對任意的，總存在，使得，求的取值范圍．

Answer 1

【答案】（1）；（2）；（3）或.

【解析】

（1）函數與軸無交點，即方程沒有實數根，即可求得的取值范圍；（2）函數的對稱軸是，所以函數在上單調遞減，則需滿足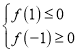；（3）根據題意可知，函數在上的函數值的取值集合是函數在上的函數值的取值集合的子集，對于函數，可分討論函數的值域，利用子集關系列不等式求的范圍.

（1）若函數的圖象與軸無關點，則方程的根的判別式，即，解得.

故的取值范圍為.

（2）因為函數的圖象的對稱軸是直線，

所以在上是減函數.

又在上存在零點，所以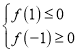，即，解得.

故的取值范圍為.

（3）若對任意的，總存在，使得，則函數在上的函數值的取值集合是函數在上的函數值的取值集合的子集.

當時，函數圖象的對稱軸是直線，所以在上的函數值的取值集合為.

①當時，，不符合題意，舍去.

②當時，在上的值域為，只需，解得.

③當時，在上的值域為，只需，解得.

綜上，的取值范圍為或.