
【題目】某學習小組在暑期社會實踐活動中,通過對某商店一種商品銷售情況的調查發現:該商品在過去的一個月內(以30天計)的日銷售價格![]() (元)與時間
(元)與時間![]() (天)的函數關系近似滿足
(天)的函數關系近似滿足![]() (
(![]() 為正常數).該商品的日銷售量
為正常數).該商品的日銷售量![]() (個)與時間
(個)與時間![]() (天)部分數據如下表所示:
(天)部分數據如下表所示:
| 10 | 20 | 25 | 30 |
| 110 | 120 | 125 | 120 |
已知第10天該商品的日銷售收入為121元.
(I)求![]() 的值;
的值;
(II)給出以下二種函數模型:
①![]() ,②
,②![]() ,
,
請你根據上表中的數據,從中選擇你認為最合適的一種函數來描述該商品的日銷售量![]() 與時間
與時間![]() 的關系,并求出該函數的解析式;
的關系,并求出該函數的解析式;
(III)求該商品的日銷售收入![]() (元)的最小值.
(元)的最小值.
(函數![]() ,在區間
,在區間![]() 上單調遞減,在區間
上單調遞減,在區間![]() 上單調遞增.性質直接應用.)
上單調遞增.性質直接應用.)
【答案】(I)1,(II) ![]() ;(III) 121元
;(III) 121元
【解析】
(I)利用![]() 列方程,解方程求得
列方程,解方程求得![]() 的值.
的值.
(II)根據題目所給表格的數據,判斷出日銷售量不單調,由此確定選擇模型②.將表格數據代入![]() ,待定系數法求得
,待定系數法求得![]() 的值,也即求得
的值,也即求得![]() 的解析式.
的解析式.
(III)將![]() 寫成分段函數的形式,由
寫成分段函數的形式,由![]() 計算出日銷售收入
計算出日銷售收入![]() 的解析式,根據函數的單調性求得
的解析式,根據函數的單調性求得![]() 的最小值.
的最小值.
(I)依題意知第10天該商品的日銷售收入為
![]() ,解得
,解得![]() .
.
(II)由題中的數據知,當時間變化時,該商品的日銷售量有增有減并不單調,故只能選②![]() .
.
從表中任意取兩組值代入可求得![]()
(III)由(2)知![]()
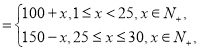
∴![]()
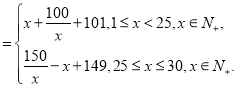
當![]() 時,
時,![]() 在區間
在區間![]() 上是單調遞減的,在區間
上是單調遞減的,在區間![]() 上是單調遞增,
上是單調遞增,
所以當![]() 時,
時,![]() 取得最小值,且
取得最小值,且![]() ;
;
當![]() 時,
時,![]() 是單調遞減的,所以當
是單調遞減的,所以當![]() 時,
時,![]() 取得最小值,且
取得最小值,且![]() .
.
綜上所述,當![]() 時,
時,![]() 取得最小值,且
取得最小值,且![]() .
.
故該商品的日銷售收入![]() 的最小值為121元.
的最小值為121元.


 文敬圖書課時先鋒系列答案
文敬圖書課時先鋒系列答案科目:高中數學 來源: 題型:
【題目】在《周易》中,長橫“![]() ”表示陽爻,兩個短橫“
”表示陽爻,兩個短橫“![]() ”表示陰爻.有放回地取陽爻和陰爻三次合成一卦,共有
”表示陰爻.有放回地取陽爻和陰爻三次合成一卦,共有![]() 種組合方法,這便是《系辭傳》所說“太極生兩儀,兩儀生四象,四象生八卦”.有放回地取陽爻和陰爻一次有2種不同的情況,有放回地取陽爻和陰爻兩次有四種情況,有放回地取陽爻和陰爻三次,八種情況.所謂的“算卦”,就是兩個八卦的疊合,即共有放回地取陽爻和陰爻六次,得到六爻,然后對應不同的解析.在一次所謂“算卦”中得到六爻,這六爻恰好有三個陽爻三個陰爻的概率是( )
種組合方法,這便是《系辭傳》所說“太極生兩儀,兩儀生四象,四象生八卦”.有放回地取陽爻和陰爻一次有2種不同的情況,有放回地取陽爻和陰爻兩次有四種情況,有放回地取陽爻和陰爻三次,八種情況.所謂的“算卦”,就是兩個八卦的疊合,即共有放回地取陽爻和陰爻六次,得到六爻,然后對應不同的解析.在一次所謂“算卦”中得到六爻,這六爻恰好有三個陽爻三個陰爻的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】根據統計,某蔬菜基地西紅柿畝產量的增加量![]() (百千克)與某種液體肥料每畝使用量
(百千克)與某種液體肥料每畝使用量![]() (千克)之間的對應數據的散點圖,如圖所示.
(千克)之間的對應數據的散點圖,如圖所示.

(1)依據數據的散點圖可以看出,可用線性回歸模型擬合![]() 與
與![]() 的關系,請計算相關系數
的關系,請計算相關系數![]() 并加以說明(若
并加以說明(若![]() ,則線性相關程度很高,可用線性回歸模型擬合);
,則線性相關程度很高,可用線性回歸模型擬合);
(2)求![]() 關于
關于![]() 的回歸方程,并預測液體肥料每畝使用量為12千克時,西紅柿畝產量的增加量
的回歸方程,并預測液體肥料每畝使用量為12千克時,西紅柿畝產量的增加量![]() 約為多少?
約為多少?
附:相關系數公式
 ,參考數據:
,參考數據:![]() ,
,![]() .
.
回歸方程![]() 中斜率和截距的最小二乘估計公式分別為:
中斜率和截距的最小二乘估計公式分別為: ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
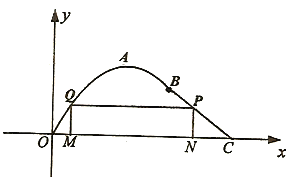
【題目】(本題16分)某鄉鎮為了進行美麗鄉村建設,規劃在長為10千米的河流OC的一側建一條觀光帶,觀光帶的前一部分為曲線段OAB,設曲線段OAB為函數![]() ,
,![]() (單位:千米)的圖象,且曲線段的頂點為
(單位:千米)的圖象,且曲線段的頂點為![]() ;觀光帶的后一部分為線段BC,如圖所示.
;觀光帶的后一部分為線段BC,如圖所示.
(1)求曲線段OABC對應的函數![]() 的解析式;
的解析式;
(2)若計劃在河流OC和觀光帶OABC之間新建一個如圖所示的矩形綠化帶MNPQ,綠化帶由線段MQ,QP, PN構成,其中點P在線段BC上.當OM長為多少時,綠化帶的總長度最長?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設兩實數![]() 不相等且均不為
不相等且均不為![]() .若函數
.若函數![]() 在
在![]() 時,函數值
時,函數值![]() 的取值區間恰為
的取值區間恰為![]() ,就稱區間
,就稱區間![]() 為
為![]() 的一個“倒域區間”.已知函數
的一個“倒域區間”.已知函數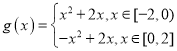 .
.
(1)求函數![]() 在
在![]() 內的“倒域區間”;
內的“倒域區間”;
(2)若函數![]() 在定義域
在定義域![]() 內所有“倒域區間”的圖象作為函數
內所有“倒域區間”的圖象作為函數![]() 的圖象,是否存在實數
的圖象,是否存在實數![]() ,使得
,使得![]() 與
與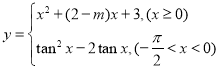 恰好有2個公共點?若存在,求出
恰好有2個公共點?若存在,求出![]() 的取值范圍:若不存在,請說明理由.
的取值范圍:若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com