解:(Ⅰ)當n=1時,a
1=5a
1+1,∴
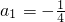
又∵a
n=5a
n+1,a
n+1=5a
n+1+1
∴a
n+1-a
n=5a
n+1,即
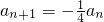
∴數列a
n成等比數列,其首項
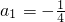
,公比是
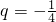
∴
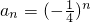
∴
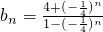
(Ⅱ)由(Ⅰ)知
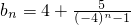
∴
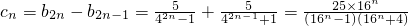
=
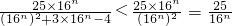
又
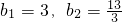
,∴
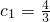
當n=1時,
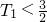
當n≥2時,
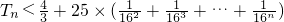
=
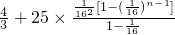
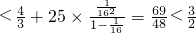
(Ⅲ)由(Ⅰ)知
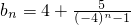
一方面,已知R
n≤λn恒成立,取n為大于1的奇數時,設n=2k+1(k∈N
+)
則R
n=b
1+b
2+…+b
2k+1=
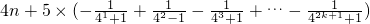
=
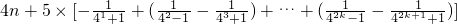
>4n-1
∴λn≥R
n>4n-1,即(λ-4)n>-1對一切大于1的奇數n恒成立
∴λ≥4否則,(λ-4)n>-1只對滿足
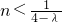
的正奇數n成立,矛盾.
另一方面,當λ=4時,對一切的正整數n都有R
n≤4n
事實上,對任意的正整數k,有
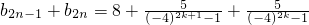
=
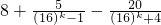
=
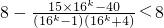
∴當n為偶數時,設n=2m(m∈N
+)
則R
n=(b
1+b
2)+(b
3+b
4)+…+(b
2n-1+b
2n)
<8m=4nw、w、w、k、s、5、u、c、o、m
當n為奇數時,設n=2m-1(m∈N
+)
則R
n=(b
1+b
2)+(b
3+b
4)+…+(b
2n-3+b
2n-2)+b
2n-1<8(m-1)+4=8m-4=4n
∴對一切的正整數n,都有R
n≤4n
綜上所述,正實數λ的最小值為4
分析:(Ⅰ)由題設條件能導出a
n+1-a
n=5a
n+1,即
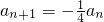
,所以
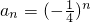
,∴
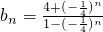
.
(Ⅱ)由
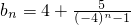
,知
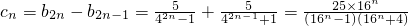
=
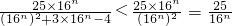
,當n=1時,
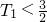
;當n≥2時,
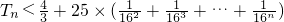
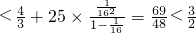
.
(Ⅲ)由
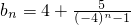
知R
n=b
1+b
2+…+b
2k+1=
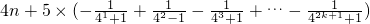
=
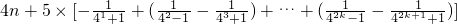
>4n-1.由此入手能推導出正實數λ的最小值為4.
點評:本題主要考查數列、不等式等基礎知識、考查化歸思想、分類整合思想,以及推理論證、分析與解決問題的能力.

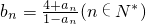 .
.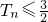 ;
;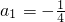
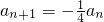
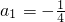 ,公比是
,公比是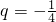
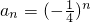
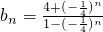
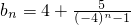
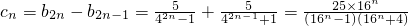
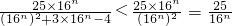
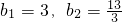 ,∴
,∴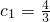
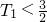
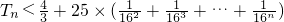
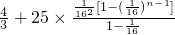
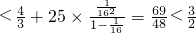
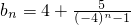
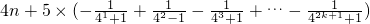
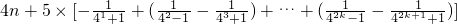
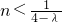 的正奇數n成立,矛盾.
的正奇數n成立,矛盾.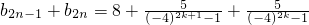
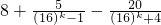
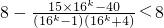
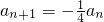 ,所以
,所以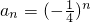 ,∴
,∴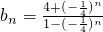 .
.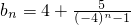 ,知
,知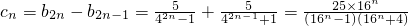 =
=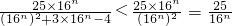 ,當n=1時,
,當n=1時,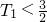 ;當n≥2時,
;當n≥2時,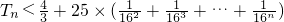
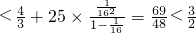 .
.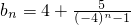 知Rn=b1+b2+…+b2k+1=
知Rn=b1+b2+…+b2k+1=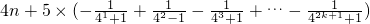 =
=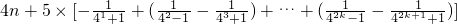 >4n-1.由此入手能推導出正實數λ的最小值為4.
>4n-1.由此入手能推導出正實數λ的最小值為4.
