
如圖所示,在矩形ABCD中,AB=a,BC=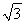 a,以對角線AC為折線將直角三角形ABC向上翻折到三角形APC的位置(B點(diǎn)與P點(diǎn)重合),P點(diǎn)在平面ACD上的射影恰好落在邊AD上的H處.
a,以對角線AC為折線將直角三角形ABC向上翻折到三角形APC的位置(B點(diǎn)與P點(diǎn)重合),P點(diǎn)在平面ACD上的射影恰好落在邊AD上的H處.
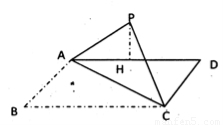
(1)求證:PA⊥CD;
(2)求直線PC與平面ACD所成角的正切值.
(1)詳見解析,(2)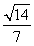 .
.
【解析】
試題分析:(1)折疊問題,首先要明確折疊前后量的變化,尤其是垂直條件的變化,本題要證明線線垂直,首先找線面垂直,因為關(guān)于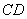 垂直條件較多,所以考慮證明
垂直條件較多,所以考慮證明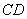
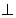 面
面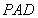 ,折疊前后都有條件
,折疊前后都有條件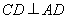 ,而折疊后
,而折疊后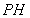
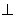 面
面 ,因此可由線面垂直得到
,因此可由線面垂直得到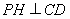 ,這樣就可由線面垂直判定定理證到
,這樣就可由線面垂直判定定理證到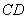
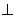 面
面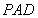 ,(2)求線面角,關(guān)鍵作出面的垂線.本題簡單,因為
,(2)求線面角,關(guān)鍵作出面的垂線.本題簡單,因為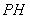
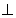 面
面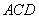 ,所以直線PC與平面ACD所成角就為
,所以直線PC與平面ACD所成角就為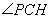 ,下面只需在直角三角形中解出
,下面只需在直角三角形中解出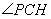 的正切值就可.
的正切值就可.
試題解析:(1) 證明: 由題設(shè),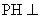 平面ACD,
平面ACD, 平面PAD
平面PAD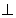 平面ACD, 3分
平面ACD, 3分
交線為AD,又CD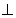 AD,
AD, CD
CD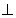 平面PAD,PA
平面PAD,PA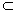 平面PAD,
平面PAD, CD
CD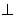 PA 6分
PA 6分
(2)連接CH,則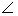 PCH為直線PC與平面ACD所成的角。
PCH為直線PC與平面ACD所成的角。
作HG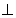 AC,垂足為G,連接PG,則AC
AC,垂足為G,連接PG,則AC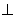 平面PHG
平面PHG  AC
AC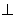 PG, 9分
PG, 9分
又在矩形ABCD中,AB=a,BC=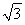 a,
a,
在直角 PGA中,PA=a,
PGA中,PA=a,
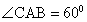
 AG=
AG=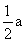
在直角 HAG中,AH=
HAG中,AH=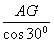 =
=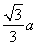 ,又AC=2a, 2分
,又AC=2a, 2分
在直角 CAH中,根據(jù)余弦定理可得,CH=
CAH中,根據(jù)余弦定理可得,CH=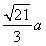 ,
,
在直角 PHA中可得PH=
PHA中可得PH=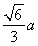 ,
, tan
tan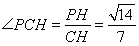 13分
13分
考點(diǎn):線面垂直判定,



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
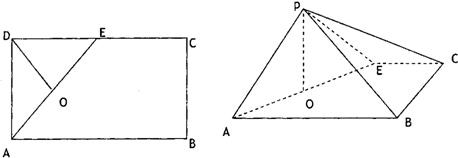
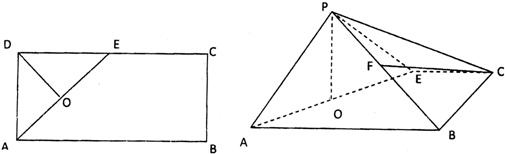 19、如圖所示,在矩形ABCD中,AB=4,AD=2,E是CD的中點(diǎn),O為AE的中點(diǎn),以AE為折痕將△ADE向上折起,使D到P點(diǎn)位置,且PC=PB,F(xiàn)是BP的中點(diǎn).
19、如圖所示,在矩形ABCD中,AB=4,AD=2,E是CD的中點(diǎn),O為AE的中點(diǎn),以AE為折痕將△ADE向上折起,使D到P點(diǎn)位置,且PC=PB,F(xiàn)是BP的中點(diǎn).查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 如圖所示,在矩形ABCD中,已知AB=a,BC=b.a(chǎn)≤3b,在AB,AD,CD,CB上分別截取AE,AH,CG,CF,且都等于x,則四邊形EFGH面積的最大值為
如圖所示,在矩形ABCD中,已知AB=a,BC=b.a(chǎn)≤3b,在AB,AD,CD,CB上分別截取AE,AH,CG,CF,且都等于x,則四邊形EFGH面積的最大值為查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com