
本小題滿分12分)設M是由滿足下列條件的函數f (x)構成的集合:①方程f (x)一x=0有實根;②函數的導數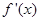 滿足0<
滿足0<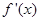 <1.
<1.
(1)若函數f(x)為集合M中的任意一個元素,證明:方程f(x)一x=0只有一個實根;
(2)判斷函數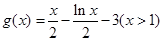 是否是集合M中的元素,并說明理由;
是否是集合M中的元素,并說明理由;
(3)設函數f(x)為集合M中的任意一個元素,對于定義域中任意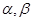 ,
,
證明: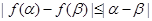
(1)令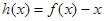 ,則
,則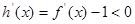 ,故
,故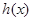 是單調遞減函數,
是單調遞減函數,
所以,方程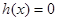 ,即
,即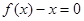 至多有一解,又由題設①知方程
至多有一解,又由題設①知方程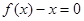 有實數根,所以,方程
有實數根,所以,方程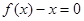 有且只有一個實數根;(2)
有且只有一個實數根;(2)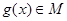 ;(Ⅲ)不妨設
;(Ⅲ)不妨設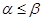 ,∵
,∵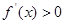 ,∴
,∴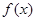 單調遞增,∴
單調遞增,∴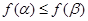 ,即
,即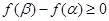 ,
,
令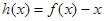 ,則
,則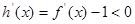 ,故
,故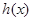 是單調遞減函數,
是單調遞減函數,
∴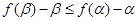 ,即
,即 ,
,
∴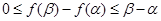 ,則有
,則有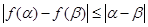
【解析】
試題分析:令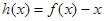 ,則
,則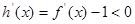 ,故
,故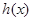 是單調遞減函數,
是單調遞減函數,
所以,方程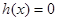 ,即
,即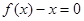 至多有一解,
至多有一解,
又由題設①知方程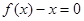 有實數根,
有實數根,
所以,方程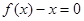 有且只有一個實數根…………………………………..4分
有且只有一個實數根…………………………………..4分
(2)易知,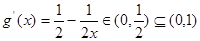 ,滿足條件②;
,滿足條件②;
令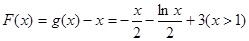 ,
,
則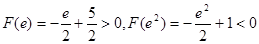 ,…………………………………..7分
,…………………………………..7分
又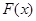 在區間
在區間 上連續,所以
上連續,所以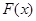 在
在 上存在零點
上存在零點 ,
,
即方程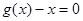 有實數根
有實數根 ,故
,故 滿足條件①,
滿足條件①,
綜上可知,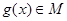 ……………………………………8分
……………………………………8分
(Ⅲ)不妨設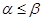 ,∵
,∵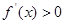 ,∴
,∴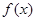 單調遞增,
單調遞增,
∴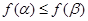 ,即
,即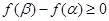 ,
,
令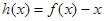 ,則
,則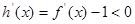 ,故
,故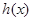 是單調遞減函數,
是單調遞減函數,
∴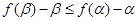 ,即
,即 ,
,
∴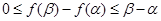 ,則有
,則有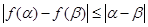 ….……………..….12分
….……………..….12分
考點:本題考查了導數的運用
點評:近幾年新課標高考對于函數與導數這一綜合問題的命制,一般以有理函數與半超越(指數、對數)函數的組合復合且含有參量的函數為背景載體,解題時要注意對數式對函數定義域的隱蔽,這類問題重點考查函數單調性、導數運算、不等式方程的求解等基本知識,注重數學思想(分類與整合、數與形的結合)方法(分析法、綜合法、反證法)的運用.把數學運算的“力量”與數學思維的“技巧”完美結合.


 互動課堂系列答案
互動課堂系列答案 激活思維智能訓練課時導學練系列答案
激活思維智能訓練課時導學練系列答案科目:高中數學 來源: 題型:
| ON |
| ON |
| 5 |
| OM |
| OT |
| M1M |
| N1N |
| OP |
| OA |
查看答案和解析>>
科目:高中數學 來源:2011屆吉林省油田中學高三第一次模擬考試數學理卷 題型:解答題
(本小題滿分12分)
設a∈R,函數f(x)= e -x(ax2 + a + 1),其中e是自然對數的底數;
(1)求函數f(x)的單調區間;
(2)當 -1<a<0 時,求函數f(x)在 [ 1,2 ] 上的最小值。
查看答案和解析>>
科目:高中數學 來源:2011-2012學年山東省高三教學質量檢測(四)文科數學試卷(解析版) 題型:解答題
(本小題滿分12分)設平面向量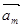 =(m,1),
=(m,1), 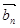 =(2,n),其中m,n∈{1,2,3,4}.
=(2,n),其中m,n∈{1,2,3,4}.
(Ⅰ)請列出有序數組(m,n)的所有可能結果;
(Ⅱ)若“使得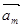 ⊥(
⊥(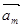 -
-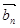 )成立的(m,n)”為事件A,求事件A發生的概率。
)成立的(m,n)”為事件A,求事件A發生的概率。
查看答案和解析>>
科目:高中數學 來源:2011-2012學年山東省萊蕪市高三上學期期末檢測理科數學 題型:解答題
(本小題滿分12分)
設 的內角A、B、C所對的邊分別為a、b、c,且
的內角A、B、C所對的邊分別為a、b、c,且 .
.
(1)當 時,求a的值;
時,求a的值;
(2)當 的面積為3時,求a+c的值。
的面積為3時,求a+c的值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com