
【題目】[選修4-4:坐標系與參數方程]
在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),直線
為參數),直線![]() 的方程為
的方程為![]() .
.
(1)以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,求曲線
軸的正半軸為極軸建立極坐標系,求曲線![]() 的極坐標方程和直線
的極坐標方程和直線![]() 的極坐標方程;
的極坐標方程;
(2)在(1)的條件下,直線![]() 的極坐標方程為
的極坐標方程為![]() ,設曲線
,設曲線![]() 與直線
與直線![]() 的交于點
的交于點![]() 和點
和點![]() ,曲線
,曲線![]() 與直線
與直線![]() 的交于點
的交于點![]() 和點
和點![]() ,求
,求![]() 的面積.
的面積.
科目:高中數學 來源: 題型:
【題目】C反應蛋白(CRP)是機體受到微生物入侵或組織損傷等炎癥性刺激時肝細胞合成的急性相蛋白,醫學認為CRP值介于0-10mg/L為正常值下面是某患者在治療期間連續5天的檢驗報告單中CRP值(單位:mg/L)與治療天數的統計數據:
治療天數x | 1 | 2 | 3 | 4 | 5 |
CRP值y | 51 | 40 | 35 | 28 | 21 |
(1)若CRP值y與治療天數x具有線性相關關系,試用最小二乘法求出y關于x的線性回歸方程,并估計該患者至少需要治療多少天CRP值可以到正常水平;
(2)為均衡城鄉保障待遇,統一保障范圍和支付標準,為參保人員提供公平的基本醫療保障.某市城鄉醫療保險實施辦法指出:門診報銷比例為50%:住院報銷比例,A類醫療機構80%,B類醫療機構60%.若張華參加了城鄉基本醫療保險,他因CRP偏高選擇在某醫療機構治療,醫生為張華提供了三種治療方案:
方案一:門診治療,預計每天診療費80元;
方案二:住院治療,A類醫療機構,入院檢查需花費600元,預計每天診療費100元;
方案三:住院治療,B類醫療機構,入院檢查需花費400元,預計每天診療費40元;
若張華需要經過連續治療n天,![]() ,請你為張華選擇最經濟實惠的治療方案.
,請你為張華選擇最經濟實惠的治療方案.
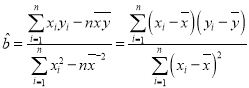 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】拋物線![]() 的焦點為
的焦點為![]() ,準線為
,準線為![]() ,若
,若![]() 為拋物線上第一象限的一動點,過
為拋物線上第一象限的一動點,過![]() 作
作![]() 的垂線交準線
的垂線交準線![]() 于點
于點![]() ,交拋物線于
,交拋物線于![]() 兩點.
兩點.
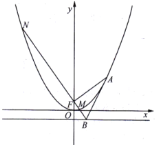
(Ⅰ)求證:直線![]() 與拋物線相切;
與拋物線相切;
(Ⅱ)若點![]() 滿足
滿足![]() ,求此時點
,求此時點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】綠水青山就是金山銀山.某山村為做好水土保持,退耕還林,在本村的山坡上種植水果,并推出山村游等旅游項目.為預估今年7月份游客購買水果的情況,隨機抽樣統計了去年7月份100名游客的購買金額.分組如下:![]() ,
,![]() ,
,![]()
![]() ,得到如圖所示的頻率分布直方圖:
,得到如圖所示的頻率分布直方圖:
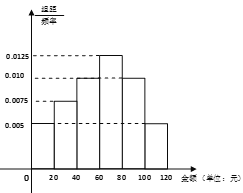
(1)請用抽樣的數據估計今年7月份游客人均購買水果的金額(同一組中的數據用該組區間中點作代表).
(2)若把去年7月份購買水果不低于80元的游客,稱為“水果達人”. 填寫下面列聯表,并根據列聯表判斷是否有95%的把握認為“水果達人”與性別有關系?
水果達人 | 非水果達人 | 合計 | |
男 | 10 | ||
女 | 30 | ||
合計 |
(3)為吸引顧客,商家特推出兩種促銷方案.方案一:每滿80元可立減10元;方案二:金額超過80元可抽獎三次,每次中獎的概率為![]() ,且每次抽獎互不影響,中獎1次打9折,中獎2次打8折,中獎3次打7折.若每斤水果10元,你打算購買12斤水果,請從實際付款金額的數學期望的角度分析應該選擇哪種優惠方案.
,且每次抽獎互不影響,中獎1次打9折,中獎2次打8折,中獎3次打7折.若每斤水果10元,你打算購買12斤水果,請從實際付款金額的數學期望的角度分析應該選擇哪種優惠方案.
附:參考公式和數據:![]() ,
,![]() .臨界值表:
.臨界值表:
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】黨的十九大報告指出,要以創新理念提升農業發展新動力,引領經濟發展走向更高形態.為進一步推進農村經濟結構調整,某村舉辦水果觀光采摘節,并推出配套鄉村游項目現統計了4月份100名游客購買水果的情況,得到如圖所示的頻率分布直方圖:
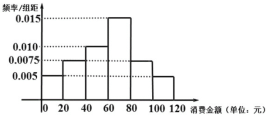
(Ⅰ)若將購買金額不低于![]() 元的游客稱為“水果達人”,現用分層抽樣的方法從樣本的“水果達人”中抽取
元的游客稱為“水果達人”,現用分層抽樣的方法從樣本的“水果達人”中抽取![]() 人,求這
人,求這![]() 人中消費金額不低于
人中消費金額不低于![]() 元的人數;
元的人數;
(Ⅱ)從(Ⅰ)中的![]() 人中抽取
人中抽取![]() 人作為幸運客戶免費參加山村旅游項目,請列出所有的基本事件,并求
人作為幸運客戶免費參加山村旅游項目,請列出所有的基本事件,并求![]() 人中至少有
人中至少有![]() 人購買金額不低于
人購買金額不低于![]() 元的概率;
元的概率;
(Ⅲ)為吸引顧客,該村特推出兩種促銷方案,
方案一:每滿![]() 元可立減
元可立減![]() 元;
元;
方案二:金額超過![]() 元但又不超過
元但又不超過![]() 元的部分打
元的部分打![]() 折,金額超過
折,金額超過![]() 元但又不超過
元但又不超過![]() 元的部分打
元的部分打![]() 折,金額超過
折,金額超過![]() 元的部分打
元的部分打![]() 折.
折.
若水果的價格為![]() 元/千克,某游客要購買
元/千克,某游客要購買![]() 千克,應該選擇哪種方案.
千克,應該選擇哪種方案.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】畫糖是一種以糖為材料在石板上進行造型的民間藝術,常見于公園與旅游景點.某師傅制作了一種新造型糖畫,為了進行合理定價先進性試銷售,其單價![]() (元)與銷量
(元)與銷量![]() (個)相關數據如下表:
(個)相關數據如下表:

(1)已知銷量![]() 與單價
與單價![]() 具有線性相關關系,求
具有線性相關關系,求![]() 關于
關于![]() 的線性相關方程;
的線性相關方程;
(2)若該新造型糖畫每個的成本為![]() 元,要使得進入售賣時利潤最大,請利用所求的線性相關關系確定單價應該定為多少元?(結果保留到整數)
元,要使得進入售賣時利潤最大,請利用所求的線性相關關系確定單價應該定為多少元?(結果保留到整數)
參考公式:線性回歸方程![]() 中斜率和截距最小二乘法估計計算公式:
中斜率和截距最小二乘法估計計算公式:

![]() .參考數據:
.參考數據:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】規定:在桌面上,用母球擊打目標球,使目標球運動,球的位置是指球心的位置,我們說球![]() 是指該球的球心點
是指該球的球心點![]() .兩球碰撞后,目標球在兩球的球心所確定的直線上運動,目標球的運動方向是指目標球被母球擊打時,母球球心所指向目標球球心的方向.所有的球都簡化為平面上半徑為1的圓,且母球與目標球有公共點時,目標球就開始運動,在桌面上建立平面直角坐標系,解決下列問題:
.兩球碰撞后,目標球在兩球的球心所確定的直線上運動,目標球的運動方向是指目標球被母球擊打時,母球球心所指向目標球球心的方向.所有的球都簡化為平面上半徑為1的圓,且母球與目標球有公共點時,目標球就開始運動,在桌面上建立平面直角坐標系,解決下列問題:
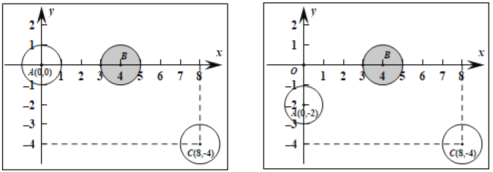
(1)如圖,設母球![]() 的位置為
的位置為![]() ,目標球
,目標球![]() 的位置為
的位置為![]() ,要使目標球
,要使目標球![]() 向
向![]() 處運動,求母球
處運動,求母球![]() 球心運動的直線方程;
球心運動的直線方程;
(2)如圖,若母球![]() 的位置為
的位置為![]() ,目標球
,目標球![]() 的位置為
的位置為![]() ,能否讓母球
,能否讓母球![]() 擊打目標
擊打目標![]() 球后,使目標
球后,使目標![]() 球向
球向![]() 處運動?
處運動?
(3)若![]() 的位置為
的位置為![]() 時,使得母球
時,使得母球![]() 擊打目標球
擊打目標球![]() 時,目標球
時,目標球![]() 運動方向可以碰到目標球
運動方向可以碰到目標球![]() ,求
,求![]() 的最小值(只需要寫出結果即可).
的最小值(只需要寫出結果即可).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,平行四邊形ABCD中,∠DAB=60°,AB=2,AD=4,將△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD.
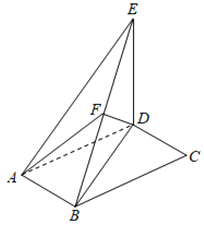
(1)求證:AB⊥DE;
(2)若點F為BE的中點,求直線AF與平面ADE所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com